Числовые множества

Понятие множества - интуитивное, не определяемое.

Множество состоит из элементов.

Множество (А) будем считать заданным, если о любом элементе известно, принадлежит он этому множеству или не принадлежит.

Множество 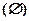будем называть пустым, если 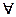элемент ему не принадлежит.

Множество может содержать конечное количество элементов (конечное множество), или бесчисленное - (бесконечное множество).

Суммой (объединением) двух множеств А и В будемназывать множество С, каждый элемент которого принадлежит хотя бы одному из слагаемых:

.

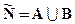Произведением (пересечением) двух множеств А и В будем называть такое множество С, каждый элемент которого принадлежит одновременно двум сомножителям:

.

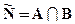Разностью двух множеств А и В будем называть такое множество С, каждый элемент которого принадлежит уменьшаемому, но не принадлежит вычитаемому:

.

.

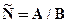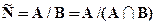Декартовым произведением двух множеств А и В будем называть множество С, состоящее из упорядоченных пар элементов данных множеств:

.

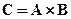Числовым множеством будем называть множество, все элементы которого являются числами.

1.1 Множество натуральных чисел

.

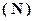
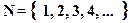Пусть .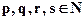

При делении p на q может произойти одно из двух:

- число p делится на число q без остатка, тогда запишем так: ;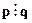

- при делении числа p на число q получается частное s и в остатке r,

тогда запишем так: .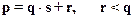

НОД (p, q) =d - наибольший общий делитель чисел p и q.

НОД (p, q) =d - это наибольшее из всех чисел, обладающих свойством:

.

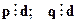Например, НОД(30, 42) = 6.

Если НОД (p, q) = 1, то будем говорить, что числа p и q взаимно просты.

НОК (p, q) = k - наименьшее общее кратное чисел p и q.

НОК (p, q) = k - это наименьшее из всех чисел, обладающих свойством:

.

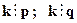Например, НОК(15, 6) = 30.

1.2. Множество целых чисел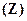

. .

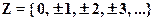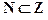1.3. Множество рациональных чисел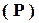

.

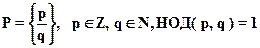P -множество всех несократимых обыкновенных дробей.

Например,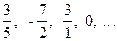

Рациональное число можно представить и десятичной дробью, либо конечной:

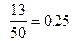, либо бесконечной периодической: .

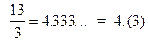1.4. Множество иррациональных чисел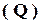

Q - это множество всех десятичных бесконечных непериодических дробей.

Например:

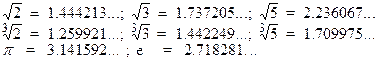
1.5. Множество вещественных (действительных) чисел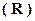

R - включает все перечисленные выше множества.

Любое вещественное число можно представить либо конечной, либо бесконечной десятичной дробью

.

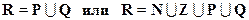1.6. Абсолютная величина числа x ()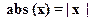

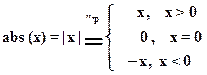
Например, | 7 | = 7; | -7 | = 7.

Свойства абсолютных величин:

1.6.1. .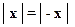

1.6.2. .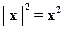

1.6.3. .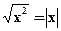

1.6.4. .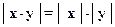

1.6.5. .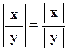

1.6.6. .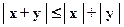

1.6.7. .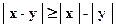

1.7. Знак числа х ( )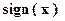

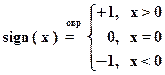
Любое вещественное число можно представить в виде:

.

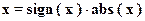Например,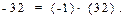

1.8. Числовые промежутки

Пусть числа 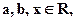причем .

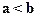Числовым промежутком будем называть множество всех вещественных чисел х,

удовлетворяющих условиям:

- конечные промежутки:

1.8.1. закрытый (замкнутый) промежуток или отрезок

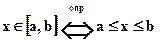
1.8.2. открытый промежуток или интервал

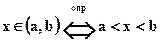
1.8.3. полузакрытый (полуоткрытый) промежуток

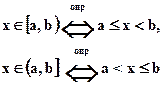
- бесконечные промежутки:

1.8.4.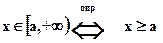

1.8.5.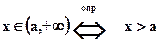

1.8.6.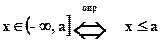

1.8.7.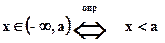

1.8.8. .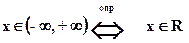

Множества 1.8.1. - 1.8.8. будем называть непрерывными, а множества - дискретными.

Дата добавления: 2014-01-07