
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторы в геометрической форме
|
|
|
|
4.1. Основные понятия
Вектором будем называть упорядоченную пару точек, первую из которых назовем началом вектора, последнюю - концом, а расстояние между ними - длиной вектора.

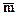 В
В
А
Обозначения:
 -вектор,
-вектор,
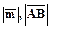 - длина вектора.
- длина вектора.
Нулевым вектором  будем называть такой вектор, у которого начало и конец совпадают. Следовательно,
будем называть такой вектор, у которого начало и конец совпадают. Следовательно,  .
.
Векторы могут быть закрепленными, скользящими и свободными.
Если векторы закрепленные, то они считаются равными только в том случае, когда совпадают их начала и совпадают концы.
Если векторы скользящие, то их можно перемещать по прямой, на которой они расположены. Такие два вектора считаются равными только в том случае, если после приведения их к общему началу путем сдвига по прямой, их содержащей, окажется, что и концы этих векторов тоже совпали.
Свободными векторами будем называть такие векторы, которые путем параллельного переноса можно произвольно перемещать в пространстве. Следовательно, можно считать, что начало свободного вектора может быть в любой точке пространства.
В дальнейшем (если не оговорено особо) будем рассматривать только свободные векторы.
Два вектора будем называть равными 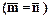 , если после параллельного переноса в общее начало окажется, что их концы тоже совпадают.
, если после параллельного переноса в общее начало окажется, что их концы тоже совпадают.
Из определения следует:  , однако, обратное утверждение не всегда справедливо.
, однако, обратное утверждение не всегда справедливо.
 Углом между двумя векторами (
Углом между двумя векторами ( 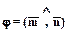 ) будем называть наименьший угол, полученный после их приведения к общему началу, причем, если направление от первого вектора ко второму идет против движения часовой стрелки, то угол будем считать положительным, а если по движению часовой стрелки, то - отрицательным.
) будем называть наименьший угол, полученный после их приведения к общему началу, причем, если направление от первого вектора ко второму идет против движения часовой стрелки, то угол будем считать положительным, а если по движению часовой стрелки, то - отрицательным.

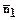

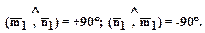

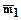
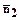



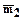



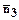
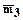

Векторы будем называть ортогональными  , если угол между ними
, если угол между ними 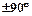 .
.
 .
.
Векторы будем называть сонаправленными (одинаково направленными)  , если угол между ними
, если угол между ними 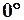 .
.
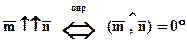 .
.
Векторы будем называть противоположно направленными  , если угол между ними
, если угол между ними 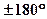 .
.
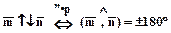 .
.
Векторы будем называть коллинеарными  , если они лежат на одной прямой или на параллельных прямых.
, если они лежат на одной прямой или на параллельных прямых.
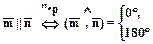
Векторы будем называть компланарными, если после приведения к общему началу окажется, что они лежат в одной плоскости.
Из определения следует, что два вектора всегда компланарны, а три и более - не обязательно.
4.2. Действия с векторами в геометрической форме
4.2.1. Сложение
Метод параллелограмма



 B C
B C


A D
 Метод цепочки R
Метод цепочки R


 N
N
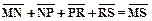
P
 M S
M S
 4.2.2. Вычитание Y
4.2.2. Вычитание Y

 X Z
X Z
4.2.3. Умножение на число (скаляр)
Произведением вектора 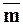 на скаляр
на скаляр 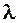 будем называть такой вектор
будем называть такой вектор ,
,
который обладает следующими свойствами:
- длина нового вектора равна длине данного вектора, умноженной на абсолютную
величину скаляра;
- направление вектора  совпадает с направлением данного вектора
совпадает с направлением данного вектора 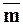 , если число
, если число 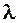 положительно или имеет противоположное ему направление, если
положительно или имеет противоположное ему направление, если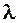 отрицательно.
отрицательно.

Из определения следует: 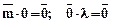 .
.
Противоположными будем называть векторы, которые равны по длине и противоположны по направлению.
Обозначение: 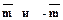 - противоположные векторы.
- противоположные векторы.
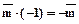 .
.
Условие коллинеарности векторов: 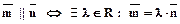 .
.
4.2.4. Умножение векторов
Существует два способа умножения вектора на вектор:
- скалярное, когда при умножении двух векторов в результате получается число (скаляр);
- векторное, когда при умножении двух векторов в результате получается новый вектор.
Скалярным произведением двух векторов (  ) будем называть число, равное произведению их длин на косинус угла между ними.
) будем называть число, равное произведению их длин на косинус угла между ними.
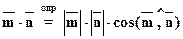 .
.
Из определения следуют свойства.
4.2.4.1. 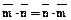 .
.
4.2.4.2. 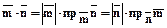 .
.
 .
.
4.2.4.3. 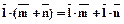 .
.
4.2.4.4. 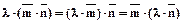 .
.
4.2.4.5. 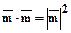 .
.
Выражение  называют скалярным квадратом вектора и используют для вычисления его длины:
называют скалярным квадратом вектора и используют для вычисления его длины:  .
.
4.2.4.6. 
Условие ортогональности векторов:
 .
.
Векторным произведением двух векторов (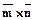 ) будем называть
) будем называть
третий вектор ( ), обладающий следующими свойствами:
), обладающий следующими свойствами:
- длина вектора  численно равна площади параллелограмма, построенного на
численно равна площади параллелограмма, построенного на
данных векторах как на сторонах;
- прямая, соединяющая концы вектора  , перпендикулярна плоскости этого
, перпендикулярна плоскости этого
параллелограмма;
- направление вектора  определяется правилом «правой руки» («буравчика»).
определяется правилом «правой руки» («буравчика»).
 B
B
 D
D




 А
А
 -
-
 S E
S E
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2450; Нарушение авторских прав?; Мы поможем в написании вашей работы!