Полные характеристики случайных величин

Законом распределения случайной величины называется всякое соотношение, устанавливающее
связь между возможными значениями случайной величины и соответствующими им вероятностями.

Простейшей формой задания этого закона
является таблица (ряд распределения), в которой перечислены возможные значения дискретной случайной величины и соответствующие им вероятности:

xi	x 1	x 2	…	xn
pi	p 1	p 2	…	pn

,

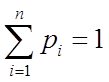
Примечание - Для непрерывной случайной величины
не существует ряда распределения

Ø Другой формой задания закона распределения является функция распределения – самая универсальная характеристика случайной величины, существующая
для дискретных и для непрерывных случайных величин:

F (x) = P (X < x),

Ø где х – некоторая текущая переменная.

Ø Функцию распределения F (x) иногда называют также интегральной функцией распределения или интегральным законом распределения.

Ø Свойства функции распределения

Ø Неубывающая функция, т.е. F (x ₁) < F (x ₂) при x ₁ < x ₂= 0

Ø F (–∞) = 0

Ø F (∞) = 1

Ø Примеры функции распределения случайных величин:

Ø 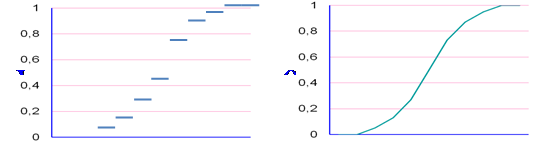Дискретной Непрерывной

По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ступенчатая кривая становится более плавной, случайная величина постепенно приближается к непрерывной величине, а её функция распределения – к непрерывной функции.

Ø Вероятность попадания случайной величины
на заданный интервал равна приращению функции распределения на этом интервале:

P (a ≤ X < b)= F (b) – F (a),

Ø т.к. (по теореме сложения вероятностей):

P (X < b)= P (a < X) + P (a ≤ X < b)

P (a ≤ X < b) = P (X < b) – P (a < X)

Ø 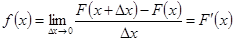Функция плотности распределения
существует только для непрерывных случайных величин и равна производной от функции распределения:

Ø Вероятность попадания случайной величины
на заданный интервал

P (a ≤ X < b)= F (b) – F (a),

Ø 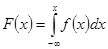может быть выражена через функцию плотности распределения на этом интервале:

Ø Откуда

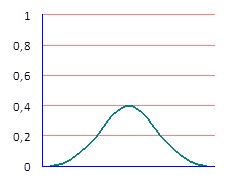
Ø Свойства функции плотности распределения

1. Функция плотности – неотрицательная функция f (x)≥0. Свойство вытекает из того, что F (x) – неубывающая функция.
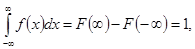2. Интеграл в бесконечных пределах от функции плотности распределения
   
   
   
   т.е. площадь фигуры, ограниченной кривой функции плотности распределения и осью абсцисс, равна 1.

Дата добавления: 2014-01-06