Спектр колебаний с угловой модуляцией

При гармоническом управляющем колебании спектр колебания с угловой модуляцией определяется выражением

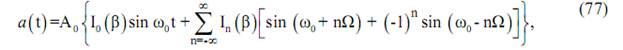
здесь 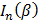– функция Бесселя первого рода n-го порядка. Таким образом, спектр колебания с УМ в общем случае содержит бесконечное число боковых составляющих .

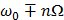Функция Бесселя являются цилиндрической функцией первого рода и выражается бесконечным сходящимся рядом

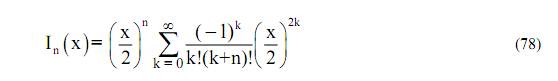
и играет такую же роль как косинусоидальные функции в декартовой системе координат. Из рис. 53 видно, что эти функции являются затухающими по амплитуде и не периодическими.

Рис. 53. Функции Бесселя

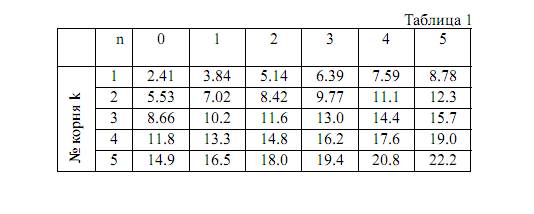
В табл. 1 приведены корни функции Бесселя различных порядков. Как видно, несущая обнуляется при β = 2.41, затем при 5.53 и т.д. Амплитуды первой пары боковых составляющих становятся равными нулю при β = 3.84, затем при 7.02 и т.д. Вторая пара боковых составляющих обнуляется при аргументе функции равным 5.14. Обобщенно следует заметить, что последующие нули будут определяться как k = (k – 1) + π.

На практике же обычно учитывается β + 1 + √β боковых составляющих при значениях 0 < β < 25, а практически учитываемая ширина спектра определяется как

Следовательно, при β << 1 ширина спектра П _ум = 2Ω и отличается от АМ–сигнала лишь изменением фазы левой боковой составляющей на 180°. При значениях

0,5≤ β ≤1 появляется вторая пара боковых и П _ум = 4Ω, для 1<β<2 и П _ум = 6Ω и т. д.

При больших значениях β>>1 ширина спектра близка к удвоенному значению девиации частоты т.к. Ω ≺≺ Δω и

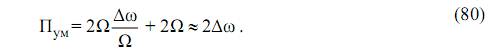
Заметим, что при малых индексах модуляции (быстрая модуляция Δω<<Ω) радиоколебание является узкополосным, а при больших индексах (медленная модуляция Δω>>Ω) – широкополосным.

Приведенные сведения о практически учитываемой ширине спектра УМ–сигналов справедливы и для негармонического сигнала.

Дата добавления: 2014-01-07