Режимы волн в линиях передачи

Любую ЛП можно представить эквивалентной длинной линией, а нерегулярности, возникающие в линии – их эквивалентными сопротивлениями в виде сосредоточенных элементов и включений. Тогда можно использовать при анализе линий передачи конечной длины основные понятия теории длинных линий. В этом случае напряжению и току в длинной линии Uи I можно поставить в соответствие электрическую E и магнитную H напряженности поля, а распределенным емкости и индуктивности – абсолютные диэлектрическую ε _a и магнитную μ _a проницаемости. Напряжение и ток в случае однородной длинной линии без потерь в любом ее сечении z (рис. 103) можно представить в виде суммы падающей и отраженной волн

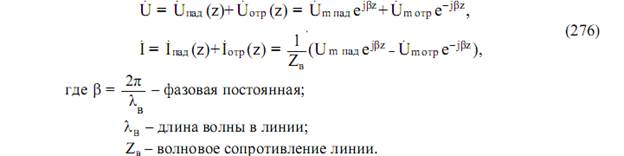
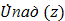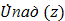Комплексная амплитуда падающей волны определяется мощностью генератора. Отношение комплексных амплитуд напряжения отраженной и падающей волн в данном сечении линии z зависит от нагрузки и называется коэффициентом отражения по напряжению:

является коэффициентом отражения от нагрузки в сечении z = 0 (где включена нагрузка линии). С учётом выражения (277) напряжение и ток в линии можно представить в виде

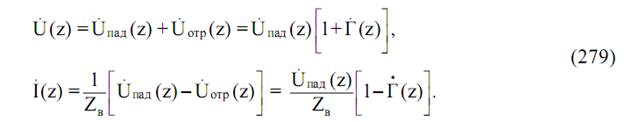
Важным параметром, характеризующим режим в длинной линии, является сопротивление Z(z), равное отношению комплексных амплитуд напряжения и тока в данном сечении линии:

или в нормированном (приведенном к волновому сопротивлению линии) виде:

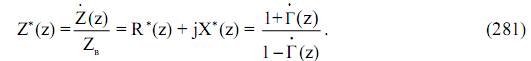
Проводимость Y(z) в данном сечении линии при этом определяется как

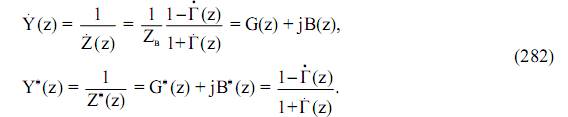
Из выражений (281) и (282) с учетом (278) можно получить

Таким образом, в каждом сечении z существует простая и однозначная связь (281), (282) между параметрами Г(z) и Z(z) или Y(z), характеризующими существующий в длинной линии режим.

На практике для определения коэффициента отражения широко используется экспериментально определенное распределение амплитуды результирующего напряжения (или тока) вдоль линии. Амплитуда результирующего напряжения в сечении z, удаленном от нагрузки к генератору на расстояние z, равна модулю напряжения (280), который в линии без потерь с учётом (278) и (279) определяется выражением

На рис. 2 представлена зависимость нормированной по отношению к амплитуде падающей волны амплитуды U_m(z) от координаты z.

Рис. 103. Распределение напряжения вдоль линии

Как видно из рис. 103, эта зависимость имеет периодический характер. Напряжение достигает минимума, равного 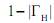, в точках, где , при

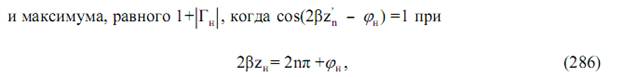
где n = 0, 1, 2, … – порядковый номер минимума или максимума, отсчитанного от нагрузки линии. Расстояние между соседними минимумами или максимумами одинаково и равно половине длины волны в данной линии.

Отношение максимального и минимального значений амплитуды напряжения называется коэффициентом стоячей волны (КСВ):

Помимо КСВ используют обратную ему величину, называемую коэффициентом бегущей волны (КБВ):

По известному значению КСВ или КБВ можно определить модуль коэффициента отражения

Аргумент коэффициента отражения от нагрузки (z = 0) можно найти из формулы:

где z ₁ - координата ближайшего к нагрузке минимума.

Рассмотренные выше параметры характеризуют режим распространения волны в длинной линии.

Если Z_н = 1, т.е. Zн = Zв, то согласно (284) . Согласованная с линией нагрузка, сопротивление которой равно волновому сопротивлению линии, не создает отраженной волны и поглощает всю мощность падающей волны. Линия с согласованной нагрузкой ведет себя подобно бесконечной регулярной линии: в ней существует режим бегущей волны, характеризуемый параметрами

'

Если нн Z= jX (сопротивление нагрузки реактивно), Z _н = 0 («короткое замыкание») или н Z= ∞ («холостой ход»), то величина , т.е. нагрузки полностью отражают падающую волну. В линии с такими нагрузками устанавливается режим стоячей волны, характеризуемый параметрами

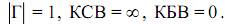
Режимы бегущей и стоячей волн являются предельными. В общем случае в линии существует так называемый смешанный режим, для которого

На рис. 104 показаны типичные графики распределения напряжения вдоль линии при различных значениях Г, получаемые из выражения (285) для передающей линии без потерь.

Рис. 104. Распределение напряжения в линии

Дата добавления: 2014-01-07