Линейная зависимость векторов

Пусть 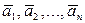- множество векторов и 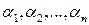-действительные числа. 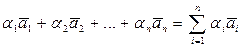- линейная комбинация векторов ,

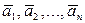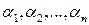- коэффициенты линейной комбинации.

О. Множество векторов 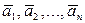называется линейно зависимым, если существует ненулевой набор чисел 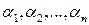, при котором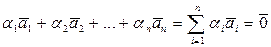

Т1 (Критерий линейной зависимости)

Множество векторов линейно зависимо тогда и только тогда, когда хотя бы один из векторов линейно выражается через остальные вектора.

Т2 (О линейно зависимой подсистеме)

Если множество векторов содержит линейно зависимое подмножество, то оно линейно зависимо.

Следствия.

1) Множество векторов, содержащее нуль-вектор линейно зависимо.

2) Если множество векторов линейно независимо, то всякое его подмножество линейно зависимо.

Т3 (О линейной зависимости 2-х векторов)

Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Лемма1 (О разложении вектора в плоскости)

Пусть векторы 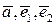компланарны и 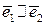. Тогда существует единственный набор чисел 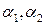такой, что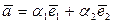

Z. Упорядоченная тройка неколлинеарных векторов - базис в плоскости этих векторов и всякий компланарный с ними вектор можно разложить по базисным векторам: 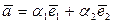, коэффициенты разложения 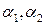называются координатами вектора 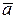в базисе .

Т4 (О линейной зависимости 3-х векторов)

Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Лемма2 (О разложении вектора в пространстве)

Пусть векторы 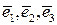некомпланарны. Тогда для любого вектора 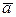найдется единственный набор чисел 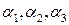такой, что .

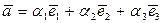Z. Упорядоченная тройка некомпланарных векторов 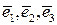- базис в пространстве и всякий вектор можно разложить по базисным векторам: 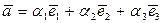, коэффициенты разложения 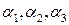называются координатами вектора 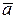в базисе .

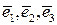Базис называется ортогональным (ОБ), если базисные векторы попарно ортогональны.

Базис называется ортонормированным (ОНБ), если базисные векторы попарно ортогональны и имеют единичную длину.

Т5 (О линейной зависимости 4-х векторов)

Всякие 4 вектора линейно зависимы.

Дата добавления: 2014-01-06