Однофакторный линейный регрессионный анализ

Применение однофакторного и многофакторного регрессионного анализа (линейная и нелинейная модели) в задачах принятия решений

В методах прогнозирования дан­ные базовой линии (временного ряда) yi(i= 1,2 ,...,m) привязываются к одинаковым временным интервалам xi (i =1,2,..., m) и зависят только от них. Но существует множество задач, в которых каждое значение у определяется целым набором независимых факторов х1, х2,..., хп, значения которых определяются не только временными интервалами. В этих случаях при моделировании неизвестных оценок У определяе­мого фактора у уже требуется учитывать взаимосвязи фактических данных. Они определяются на основе взятых из наблюдений данных, которые задаются следующей матрицей:

У 1	х 11	х 12	…	х1п
У 2	x 21	x 22	…	х 2 п
…	…	…	…	…
ут	хт 1	хт 2	…	хтп

В таких задачах используют метод регрессионного анализа.

Рег­рессия - это статистический метод, позволяющий найти уравнение, которое наилучшим образом описывает множество данных. Уравне­ние регрессии

Y=f(x1,x2..., xn) (2)

выбирают исходя из характера взаимосвязей (наблюдаемого в опыте или на графиках). Параметры уравнения (коэффициенты, свободный член) находят по методу наименьших квадратов, находя сумму квад­ратов отклонений L фактических значений yi от найденных Уi; по уравнению регрессии (2) при значениях факторов xik, взятых из мат­рицы (1):

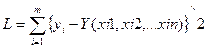
и затем минимизация ее: L ->0.

Регрессионный анализ позволяет исследовать линейные и нели­нейные взаимосвязи между задаваемыми факторами х 1, х 2 ,..., хn и определяемым фактором у. Этот метод применяют как для прогнози­рования, гак и для оценки значений у при варьировании факторов х 1, х 2,..., хп внутри интервалов их допустимых значений, например, для принятия решений по вопросам финансирования операций, проведе­ния маркетинговых исследований и т. п.

Excel предоставляет следующие возможности для анализа:

• инструменты Пакета анализа (Регрессия и др.);

• функции ЛИНЕЙН, ТЕНДЕНЦИЯ, ЛГРФПРИБЛ для построения уравнений регрессий;

• функции FPACIT, СТЬЮДРАСП для оценки достоверности уравнения регрессии и его коэффициентов;

• диаграммы и линии тренда для графической иллюстрации взаи­мосвязей.

Регрессия называется однофакторной (или парной), если она опи­сывает зависимость между функцией и одной переменной. При одно­факторном анализе в матрице (1) остаются только первый и второй столбцы данных, а уравнение регрессии (2) выглядит как у=f(х 1 ) или просто y=f(x). Оно может быть как линейным у=а*х+в, так и нелиней­ным.

Для получения уравнения регрессии необходимо:

• определить значения коэффициентов в уравнении;

• оценить достоверность полученного уравнения.

Дата добавления: 2014-01-06