Задачи линейного программирования

Структура и классификация систем массового обслуживания

Задачи оптимизации в экономических исследованиях

Тема 2.3 Задачи оптимизации

Линейная множественная регрессия

С помощью функции ЛГРФПРИБЛ

Однофакторный нелинейный регрессионный анализ

Для нахождения уравнения нелинейной регрессии в Excel приме­няется функция ЛГРФПРИБЛ, которая обеспечивает получение урав­нения регрессии в виде

y=e*OT^.

Регрессия называется множественной, если она описывает зависи­мость функции от нескольких переменных и имеет вид

У = f (x 1, x 2,..., xn).

1. Структура и классификация систем массового обслуживания

2. Надстройка Excel ''Поиск решения''

Многие экономические задачи связаны с системами массового обслуживания (СМО). В таких системах, с одной стороны, возникают массовые запросы на выполнение каких-либо услуг, с другой — происходит удовлетворение этих запросов. Примерами систем массового обслуживания могут служить торговля, склады и базы, организации бытового обслуживания населения, телефонные станции, ремонтные мастерские и пр.

Исследованием СМО занимается теория массового обслуживания. Методами теории массового обслуживания исследуются многие процессы, происходящие в экономике. Так, в организации торговли эти методы позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и другие параметры. Основной задачей теории массового обслуживания является расчет оптимальных соотношений между числом поступающих требований на обслуживание и числом обслуживающих устройств, при которых суммарные расходы на обслуживание и убытки от простоя были бы минимальными, а эффективность работы СМО — максимальной.

Обслуживающие устройства (станки, кассы, телефонные линии, диспетчеры, продавцы) в теории массового обслуживания называются каналами обслуживания. Массовые заявки (требования) на выполнение услуг образуют входящий поток, обслуженные требования — выходящий поток. Поскольку входящий поток и обслуживание требований в СМО являются, как правило, процессами случайными, то для их описания привлекаются законы распределения случайных величин.

Теоретически наиболее разработаны и удобны в практическом применении методы решения таких задач обслуживания, в которых входящий поток требований является простейшим. Для простейшего потока выполняются свойства стационарности и ординарности и отсутствует последействие (такой поток, например, характерен для большинства процессов в торговле). Простейший поток описывается законом распределения Пуассона. Обслуживание требований в системе чаще всего задается показательным законом. На основе этих законов выводятся формулы для расчета параметров работы СМО.

Пусть l — среднее количество требований, поступающих в систему в единицу времени, m — среднее количество требований, обслуживаемых в системе одним каналом в единицу времени. Эти величины находятся по данным наблюдений в СМО и являются исходными параметрами для моделирования. Вместо m часто вводят среднее время обслуживания одного требования одним каналом (t_o6сл). Параметры m и t_o6сл связаны соотношением .

Введем обозначение: . Величина a определяет среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступающие требования. СМО с n каналами будет эффективно работать, если 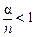. Это означает, что число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования.

Различают СМО одноканальные и многоканальные, СМО с отказом и СМО с очередью. В СМО с отказом требование не обслуживается, если на момент его поступления все каналы оказываются занятыми. Такое требование выходит из системы и теряется (например, звонок в телефонной сети). В СМО с очередью требование становится в очередь и обслуживается по мере освобождения любого из каналов (например, очередь на ремонт). Очередь бывает ограниченной или неограниченной. Среднеожидаемые характеристики работы СМО и расчетные формулы определяются типом СМО. Для СМО с неограниченной очередью параметры работы определяются предельными вероятностями состояний системы.

Рассмотрим случай многоканальной СМО с неограниченной очередью. В такой СМО все поступающие требования принимаются
в систему, следовательно, вероятность отказа (Р_отк) равна 0. Веро-
ятность того, что поступившее в систему требование будет принято
к обслуживанию, дополняет вероятность отказа до единицы:
Р_отк + Р_обсл = 1. Следовательно, для данной СМО Р_обсл = 1. Абсолютная пропускная способность системы равна А = l · q = l.

Найдем следующие характеристики работы такой СМО при .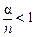

Вероятность того, что все обслуживающие каналы свободны (Р_о), исчисляется по формуле

(1)

Вероятность того, что все обслуживающие каналы заняты и r требований находится в очереди (P_n+r), рассчитывается по формуле

(2)

Среднее число занятых каналов (К_з) можно представить в виде следующих соотношений:

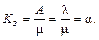
Среднее число требований, находящихся в очереди (длина очереди) (L_oч), исчисляется с помощью следующей формулы:

(3)

Среднее число требований, находящихся в системе (K), рассчитывается с помощью формулы

.

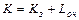Среднее время пребывания требования в очереди (t_ож) вычисляется с использованием формулы

.

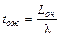Среднее время пребывания требования в системе (t_сист) определяется по формуле

.

2. Надстройка Excel ''Поиск решения''

Все приложения Microsoft Office имеют надстройки. Надстройка — это некоторая дополнительная программа, которая расширяет функциональные возможности основного приложения.

Основные принципы использования надстроек.

1. надстройка должна быть установлена. Установка подразумевает копирование файла надстройки на жесткий диск компьютера и, возможно, регистрацию надстройки в реестре Windows. Этот процесс выполняется во время установки Microsoft Office.

2. установленная надстройка должна быть загружена. Загрузка подразумевает копирование надстройки в оперативную память компьютера, после чего функции надстройки могут быть использованы.

3. Операция, противоположная загрузке, называется выгрузка. При выгрузке надстройка удаляется из оперативной памяти (на диске надстройка остается) и освобождаются все занятые ею ресурсы компьютера.

Загрузка и выгрузка надстроек в Excel выполняется с помощью диалогового окна Надстройки, которое открывается с помощью команды Сервис|Надстройки…

Чтобы загрузить надстройку, нужно установить флажок рядом с ее названием, а чтобы выгрузить надстройку, нужно этот флажок снять (и нажать кнопку ОК).

Для того чтобы использовать надстройку "Поиск решения", от пользователя требуется лишь умение с помощью серии диалоговых окон правильно сформулировать условия задачи, и если решение существует, то "Поиск решения" отыщет его.

Задачи, для решения которых можно воспользоваться надстройкой "Поиск решения", имеют ряд общих свойств:

· Имеется единственная целевая ячейка, содержащая формулу, значение которой должно быть сделано максимальным, минимальным или же равным какому-то конкретному значению. Эта формула может, например, служить для вычисления чистой прибыли или общих транспортных расходов.

· Формула в этой целевой ячейке содержит ссылки (прямые или косвенные) на ряд изменяемых ячеек (содержащих неизвестные, или переменные решаемой задачи). Поиск решения заключается в том, чтобы подобрать такие значения этих переменных, которые бы давали оптимальное значение для формулы в целевой ячейке. Изменяемые ячейки могут содержать, например, себестоимость или цену товаров, транспортные тарифы или налоговые ставки.

· Кроме того, может быть задано некоторое количество ограничений — условий или соотношений, которым должны удовлетворять некоторые из изменяемых ячеек. Например, можно потребовать, чтобы общие затраты не превосходили 100 000 000 рублей или чтобы затраты на рекламную кампанию составляли от 10 до 15 % от общих расходов.

Круг подобных задач достаточно широк. Например, транспортная задача.

Ее формулировка состоит в следующем. Имеется несколько пунктов производства и пунктов потребления некоторого продукта. Для каждого из пунктов производства задан объем производства, а для каждого пункта потребления — объем потребления. Известна также стоимость перевозки из каждого пункта производства в каждый пункт потребления единицы продукта. Требуется составить план перевозок продукта, в котором все пункты потребления были бы обеспечены необходимыми продуктами, ни из какого пункта производства не вывозилось бы продуктов больше, чем там производится, а стоимость перевозки была бы минимальной.

Дата добавления: 2014-01-06