Лекция 10. (1) и (2) – система алгебраических уравнений, с помощью которой можно определить любую переменную yi(p)

Но схема – не самоцель.

(1) и (2) – система алгебраических уравнений, с помощью которой можно определить любую переменную y_i(p), 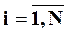, через изображения внешних воздействий 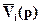. Подставляя (1) в (2)

и разрешая полученное уравнение относительно , получаем систему из N уравнений с N неизвестными y_i(p), :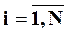

,

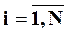
Для получения уравнения САУ используют преобразования структурных схем, т.е. соединения звеньев заменяют одним звеном с эквивалентной ПФ. Проводя несколько раз подобную операцию, приходят к простому соединению звеньев.

Правила преобразования структурных схем.

1. Последовательное соединение - это соединение, при котором выходная величина каждого предыдущего звена является входом последующего. Рассмотрим соединение двух звеньев N=2:

y₁=W₁v₁; y₂=W₂v₂ (3);

Для последовательного соединения уравнения связи и уравнение выхода имеют следующий вид

v=v₁; v₂=y₁; y₂=y.

Здесь v – вход и y –выход последовательного соединения звеньев. Построим структурную схему этого соединения, представленную ниже

Найдем W – ПФ звена, эквивалентного последовательному соединению.

Т.к.

; W₁=y₁/v₁; W₂=y₂/v₂,

то

Вывод: Передаточная функция последовательного соединения звеньев равна произведению передаточных функций звеньев, образующих это соединение.

Для последовательного соединения N звеньев:

W=W₁*W ₂*…*W_N=

2. Параллельное соединение – входная величина соединения поступает на несколько звеньев, а выходные сигналы этих звеньев суммируются.

Пусть 2 звена описываются уравнением y₁=W₁v₁; y₂=W₂v₂ (3), уравнение связи v=v₁=v₂, уравнение выхода y=y₁+y₂. Построим структурную схему параллельного соединения звеньев.

Найдем ПФ параллельного соединения звеньев:

W=y/v=(y₁+y₂)/v=y₁/v + y₂/v=W₁+W₂.

Следовательно, передаточная функция параллельного соединения звеньев равна сумме передаточных функций звеньев, входящих в соединение:

Для параллельного соединения N звеньев:

W=W₁+W₂+…+W_N=

3. Соединение звеньев с ОС.

Пусть 2 звена описываются уравнением y₁=W₁v₁; y₂=W₂v₂ (3). Для соединения с обратной связью уравнения связи v₁=v (±)y₂; v₂=y₁=y.

Здесь (-) – ООС; (+) – ПОС. Построим структурную схему соединения с обратной связью.

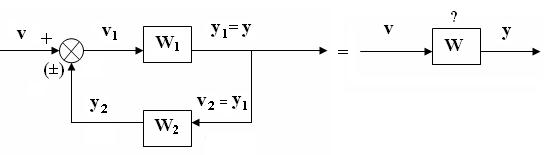
W₁ – ПФ прямой связи, W₂ – ПФ обратной связи.

Найдем ПФ соединения с обратной связью:

Отсюда ПФ соединения с обратной связью имеет вид

Здесь знак – соответствует положительной ОС, знак + соответствует отрицательной ОС.

В ряде случаев называют W – ПФ замкнутого контура.

Для получения ПФ разомкнутого контура разрывают ОС: получается последовательное соединение двух звеньев Wp=W1*W2 – ПФ разомкнутого контура.

Если W₂=1, то называют соединение звеньев с единичной ОС.

4. Перемещение элементов суммирования.

а) на выход звена (по ходу сигнала)

y=W(v₁+v₂)=Wv₁+Wv₂.

б) на вход звена (против хода сигнала)

y=Wv₁+v₂ =W(v₁+ 1/W *v₂).

5. Перемещение точек съема.

а) на выход звена (по ходу сигнала)

б) на вход звена (против хода сигнала)

6. Перестановка элементов суммирования и точек съема

а) перестановка элементов суммирования

v₄ = (v₁ –v₃)-v₂ = (v₁-v₂) –v₃

б) перестановка точек съема

Алгоритм преобразования структурной схемы:

1) Развязать перекрещивающиеся контуры ОС (правила 4-6).

Рекомендация: как правило, переносят элементы суммирования против хода сигнала, а точки съема по ходу сигнала.

2) Заменить каждое из соединений звеньев одним звеном с эквивалентной ПФ (правила 1-3).

Пример: Трехконтурная структурная схема. Надо найти ПФ системы Ф=y/v.

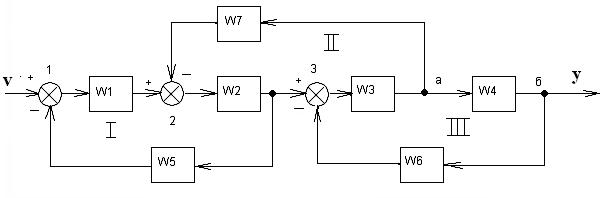
1) Переносим элемент суммирования 2 на вход звена W1, а затем меняем местами 1-ый и 2-ой элементы суммирования.

2) Переместим точку съема «а» на выход звена W4, а затем поменяем местами точки «а» и «б».

При этом получаем преобразованную структурную схему:

Используя правила (1) и (3), находим

W8=W1*W2/(1+W1*W2*W5);

W9=W3*W4/(1+W3*W4*W6);

W10=W7/(W1*W4).

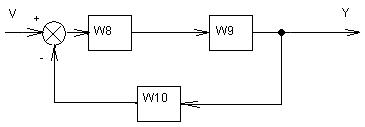
Ф =y/v=W8*W9/(1+W8*W9*W10)

Дата добавления: 2014-01-07