Уравнения и ПФ одноконтурных САУ

Лекция 11

1. Типовые структурные схемы замкнутой системы.

После преобразования структуры ОУ к одному звену выбирается закон управления, который определяет структурную схему системы управления. Рассмотрим типовые структурные схемы, соответствующие типовым законам управления.

a) Управление с прямой и обратной связью

Рис. 1. Типовая схема САУ с прямой и обратной схемой.

На этом рис. v(p) – изображение по Лапласу задающего воздействия v(t); f(p) - изображение по Лапласу возмущающего воздействия f(t), эквивалентного по своему влиянию нескольким возмущающим воздействиям, обычно влияющим на работу САУ; s(p) - изображение по Лапласу шума измерения s(t); - изображение по Лапласу наблюдаемого сигнала ; y(р) – изображение управляемой величины y(t), причем обычно =y(t)+s(t); u(p) – изображение управляющего воздействия (управления) u(t); u₂(p)- изображение сигнала прямой связи u₂(t); u_ос(p)- изображение сигнала обратной связи u_ос(t); W₁ (p) – ПФ ОУ.

Если положить f=s=0, то получаем закон управления (в изображениях) с прямой и обратной связью:

u(p)=W₂(p)v(p) - W_β(p)y(p),

описывающий работу управляющего устройства.

Здесь W₂ (p) – ПФ прямой связи (ПФ управляющего устройства по задающему воздействию), W_β(p) – ПФ обратной связи (ПФ управляющего устройства по выходной, управляемой величине). Звено прямой связи также называют предварительным фильтром.

В связи с тем, что имеются две передаточные функции W₂(p), W_β(p), с помощью которых можно влиять на свойства проектируемой системы, данную структуру называют системой с двумя степенями свободы. При этом открывается возможность решать независимо две задачи:

1. уменьшить влияние на управляемую величину возмущающего воздействия, шума измерения и неопределенности модели объекта управления за счет выбора обратной связи в отсутствие задающего воздействия и

2. добиться желаемой точности воспроизведения задающего воздействия с помощью прямой связи, не принимая во внимание факторы, упомянутые в первой задаче.

Эта структурная схема соответствует системе с неединичной обратной связью.

В ряде случаев применяют эквивалентную при W₂(p)= W_ф(p) * W_β(p) структуру с двумя степенями свободы, представленную на рисунке ниже.

b) Управление по ошибке

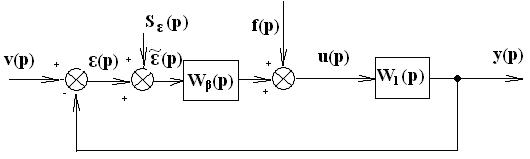
Рис. 2

При этом структурная схема получается из схемы (рис. 1) при W₂(p)= W_β(p), . Здесь - изображение ошибки управления . На выходе датчика ошибки (сравнивающего устройства) получаем сигнал ошибки

,

где - изображение шума измерения ошибки 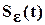. Здесь закон управления (при 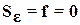) описывается выражением:

u(p)= W_β(p)* .

Такой закон называется законом управления по ошибке. Его удобно использовать тогда, когда не удается измерить задающее воздействие, а можно лишь измерить разность v(t) и y(t).

В связи с тем, что для изменения свойств системы используется лишь одна передаточная функция W_β(p) такую систему называют системой с одной степенью свободы.

Во многих случаях применяют развернутую модель объекта управления

y(p)= W₁ (p) u(p)+ W₁^f (p)f(p),

где W₁^f(p) называется передаточной функцией ОУ по возмущающему воздействию. Этой модели соответствует структурная схема

Тогда возмущающее воздействие приложено к выходу ОУ.

2. Передаточные функции замкнутой одноконтурной САУ

На САУ влияет 3 внешних воздействия – задающее, возмущающее и шум измерения.

Поэтому различают 3 ПФ:

1) ПФ по задающему воздействию (ПФ замкнутой системы) – это отношение изображения по Лапласу управляемой величины предварительно невозбужденной системы к задающему воздействию в отсутствие других внешних воздействий.

Ф(р)= . (1)

Выразим Ф(р) через передаточные функции звеньев, входящих в структурные схемы на рис.1 и рис.2.

При f=s=0 структурная схема (рис. 1) принимает вид

Используя правила преобразования структурных схем, находим ПФ по задающему воздействию

.

ПФ разомкнутого контура ОС:

W(р)=.

Для структуры, представленной на рис. 1,

W(p)=W₁(p)W_β(p). (*)

С учетом выражения (*) ПФ замкнутой системы по задающему воздействию можно записать так:

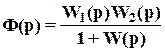. (2)

Структуру системы с единичной ОС, изображенной на рис. 2, при 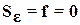, легко преобразовать к виду, называемому структурой Блэка:

Здесь ПФ W(p) определяется по (*) и называется ПФ разомкнутой системы. В случае единичной обратной связи ПФ по задающему воздействию определяется как

(**)

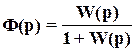и называется передаточной функцией замкнутой системы.

Как видим, в этом случае ПФ замкнутой системы полностью выражается через ПФ разомкнутой системы.

Реакцию системы на отдельно взятое задающее воздействие часто обозначают с индексом v, т.е. в виде

y(p)=y_v(p).

2) ПФ по возмущающему воздействию (по возмущению) - это отношение изображения по Лапласу управляемой величины к возмущающему воздействию предварительно невозбужденной системы в отсутствие других внешних воздействий.

Согласно определению эта ПФ записывается так:

Ф_f(р)=. (3)

Выразим Ф_f(р) через ПФ ОС и ПФ ОУ. С этой целью преобразуем структурную схему (рис. 1)

к другому виду, а именно,

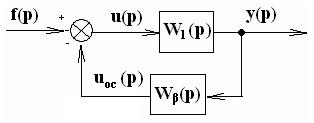
считая входом f(p) и учитывая, что v=s=0.

Также учитываем, что

u(p)=f(p) - u_oc(p)

Используя правило, относящееся к соединению звеньев с ОС, получаем

, (4)

где W(p) определяется по выражению (*).

ПФ по возмущению для системы с единичной ОС не отличается от выражения (4).

Реакция системы на отдельно взятое возмущающее воздействие обозначается с индексом f, т.е. как

y(p)=y_f(p).

3) ПФ по шуму измерения - это отношение изображения по Лапласу управляемой величины к шуму измерения предварительно невозбужденной системы в отсутствие других внешних воздействий.

Формально ПФ по возмущению выглядит так:

Ф_s(р)=. (5)

Считая входом системы, шум измерения и учитывая отсутствие других внешних воздействий, преобразуем структуру, представленную на рис. 1,

к следующему виду:

Используя выражения для ПФ соединения звеньев с положительной ОС, получаем

или

. (6)

Для системы с единичной ОС ПФ по шуму измерения ошибки

Ф_sε(р)=

равняется ПФ замкнутой системы, т.е. Ф_sε(р)=Ф(р).

Реакция системы на отдельно взятый шум измерения обозначается как

y(p)=y_s(p).

4) Передаточная функция, связывающая управление и шум измерения предварительно невозбужденной системы в отсутствие других внешних воздействий,

Ф_us(р)=.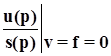

Она связана с ПФ прямой и обратной связи соотношением

.

Замечание. Все эти четыре передаточных функции должны обязательно приниматься во внимание при проектировании системы. В большинстве учебников уделяется лишь внимание ПФ по задающему воздействию, которая не отражает всех свойств системы.

Стандартная форма представления ПФ разомкнутой системы (контура)

ПФ разомкнутой системы W(p)=y(p)/ε(p) вычисляется в результате алгебраических операций над передаточными функциями звеньев W_i(p)=K_i(p)/D_i(p), , каждая из которых представляет собой отношение многочленов от р.

Следовательно, ПФ разомкнутой системы также можно представить в виде отношения двух многочленов

W(p)=K(p)/D(p).

В теории управления принято записывать эту ПФ в стандартной форме, т.е. как

,

где – нормированная ПФ разомкнутой системы, удовлетворяющая условию W₀(0)=1; ν – число интегрирующих звеньев, входящих в ПФ, от числа интегрирующих звеньев зависит точность системы; k – коэффициент усиления разомкнутой системы (контура), определяемый выражением

.

Выясним физический смысл коэффициента усиления. Для этого, используя выражение

найдем уравнение разомкнутой системы в изображениях

.

Здесь представляет собой преобразование Лапласа от ν -той производной управляемой величины предварительно невозбужденной системы.

Пусть ошибка является постоянным сигналом ε(t)=ε₀=const, так что ее изображение ε(р)= ε₀/р. При этом установившееся значение ν -ой производной находим по теореме о конечном значении:

==.

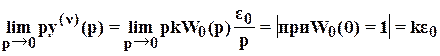Отсюда, коэффициент усиления разомкнутой системы представляет собой отношение установившегося значения ν-ой производной ее реакции и постоянного входного сигнала:

Дата добавления: 2014-01-07