Дифференциальное уравнение замкнутой системы

ДУ системы – это уравнение, связывающее между собой y(t) c v(t), f(t), s(t). ДУ можно определить с помощью структурной схемы (рис. 1)

по известным ПФ ее звеньев. Предположим, что найдены в виде отношения многочленов

ПФ ОУ

,

ПФ прямой связи

,

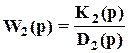ПФ ОС

.

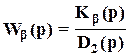При этом

1+W(p)=1+,

где

Д(р) = 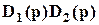+. (8)

В соответствии с (2) 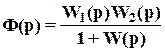ПФ по задающему воздействию

. (9)

В соответствии с (4) ПФ по возмущающему воздействию

. (10)

В соответствии с (6) ПФ по шуму измерения

. (11)

Если числители этих ПФ не содержат общих делителей со знаменателем Д(р), то Д(р) – характеристический многочлен замкнутой системы.

Пример. ; Д(р)= 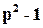, р+1≠Д(р).

Из (7) y(р)=Ф(р)v(p)+Ф_f(р)f(p)+Ф_s(p)s(p) с учетом (9-11) после умножения на Д(р) получаем уравнение замкнутой системы в изображениях

Д(р)y(р)=K₁(р)K₂(р)v(р)+K₁(р)D₂(р)f(p) - K₁(р)K_β(р)s(p). (12)

Если правая часть равна нулю, то Д(р)y(р)=0 – уравнение замкнутой автономной системы в изображениях (т.е системы в отсутствие всех внешних воздействий). Заменяя в (12) изображения сигналов оригиналами и многочлены от р операторными многочленами, получаем дифференциальное уравнение замкнутой системы, записанное в операторной (символической) форме

Д(D)y(t)=K₁(D)K₂(D)v(t)+K₁(D)D₂(D)f(t) - K₁(D)K_β(D)s(t). (13)

Здесь D – оператор дифференцирования.

Пример. Пусть ПФ

, , .

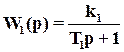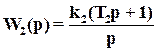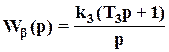В этом случае

K₁(p)= 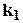; K₂(p)=k₂(T₂p+1); 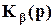=k₃(T₃p+1); D₁(p)=T₁p+1; D₂(p)=p.

Согласно (8)

Д(р)= 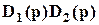+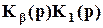=(T₁p+1)р+ k₁k₃(T₃p+1)=

=T₁p²+(1+k₁k₃T₃)p+k₁k₃.

Пусть s=0. В соответствии с (12)

Д(р)y(р)=K₁(р)K₂(р)v(р)+K₁(р)D₂(р)f(p)-K₁(р)K_β(р)s(p) и (13) Д(D)y(t)=K₁(D)K₂(D)v(t)+K₁(D)D₂(D)f(t)-K₁(D)K_β(D)s(t) находим уравнение замкнутой системы в изображениях

[T₁p²+(1+k₁k₃T₃)p+k₁k₃]y(p)=k₁k₂(T₂p+1)v(p)+k₁pf(p),

в операторной форме

[T₁D²+(1+k₁k₃T₃)D+k₁k₃]y(t)=k₁k₂(T₂D+1)v(t)+k₁Df(t)

и в оригиналах

Дата добавления: 2014-01-07