Ошибка по возмущению

Методика определения установившейся ошибки по возмущению ε_fуст принципиально не отличается от рассмотренных способов определения установившейся ошибки воспроизведения. При типовых возмущающих сигналах вида степенных функций 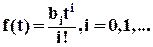используют теорему о конечном значении, согласно которой

ε_fуст= 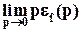. (38)

В случае воздействия на систему одного возмущения f(t) с учетом (5) получим

ε_fуст= -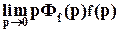. (39)

Если же возмущение f(t) – медленно меняющийся сигнал, представляемый конечным числом слагаемых ряда Тейлора

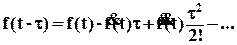, (40)

то установившаяся ошибка по возмущению вычисляется по формуле

ε_fуст(t)=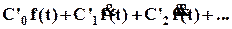, (41)

где коэффициенты C’₀, C’₁, C’₂,… представляют собой коэффициенты ошибок по возмущению, определяемые по формуле

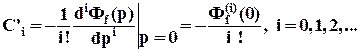(42)

Коэффициенты ошибок по возмущению С’_i в общем случае отличаются от коэффициентов ошибок воспроизведения С_i. Поэтому требует уточнения ранее сформулированное определение статических и астатических систем. Все, что говорилось ранее по данному вопросу, справедливо для систем, астатических по отношению к входному сигналу. Так, если С₀=0, С₁≠0 то система имеет астатизм первого порядка по отношению к входу; если С₀=С₁=0, C₂ ≠0, то система обладает астатизмом второго порядка относительно входного сигнала.

Теперь введем понятие астатизма системы по отношению к возмущению. Системы, для которых С’₀=0, называются астатическими по отношению к возмущению и с астатизмом первого порядка, если 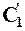≠0. Такие системы полностью устраняют влияние на управляемую величину в установившемся состоянии постоянных возмущений f(t)=f₀=const ( см. рисунок ниже ).

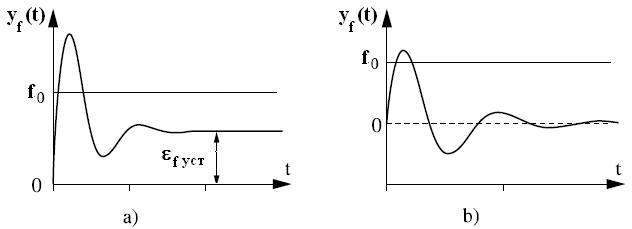
Наконец, системой ν_f -го порядка астатизма по отношению к возмущению называется система, для которой

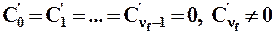. (43)

Дата добавления: 2014-01-07