Обеспечение астатизма по возмущающему воздействию

Лекция 22

Рассмотрим вопрос о том, каким образом можно обеспечить астатизм системы по возмущению. С этой целью исследуем систему, структура которой представлена на рис. 3. Пусть передаточная функция объекта W₁(p) включает ν₁ интегрирующих звеньев, а передаточная функция управляющего устройства W₂(p) – ν₂ интегрирующих звеньев, так что

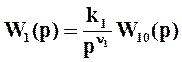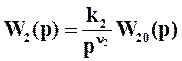, , (43а)

причем W₁₀(0)=W₂₀(0)=1.

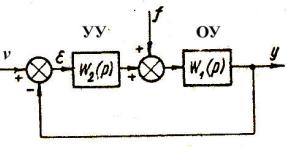
Рис. 3.

Докажем, что порядок астатизма системы по возмущению определяется числом интегрирующих звеньев ν₂, содержащихся в звене УУ, расположенном между входом системы и точкой приложения возмущения, т.е. докажем, что при ошибка ε_fуст=0, если ν₂>i.

Передаточная функция по возмущению с учетом (43a)

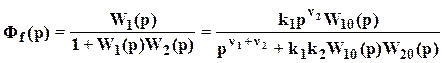. (44)

Подставляя полученное выражение в формулу (39) ε_fуст= -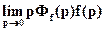, находим

ε_fуст = 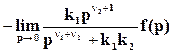. (45)

Учитывая, что , получим

ε_fуст = 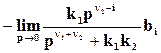. (46)

Отсюда

ε_fуст = 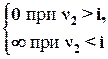(47)

независимо от величины ν₁.

Следовательно, число ν₂ первых коэффициентов ошибок по возмущению равны нулю, т.е.

С’_i=0, i=0,1,…, ν₂-1,

и система имеет порядок астатизма ν_f = ν₂ по отношению к возмущению f(t).

Если элемент с передаточной функцией W₂(p) не содержит интегрирующих звеньев, то наличие последних в элементе с передаточной функцией W₁(p) не может придать системе астатизм по возмущению. Заметим, что порядок астатизма системы по отношению к входному сигналу определяется общим числом интегрирующих звеньев, т.е. величиной ν=ν₁+ν₂.

Если ν₂=i, то ошибка по возмущению – постоянная величина, определяемая выражением

ε_fуст =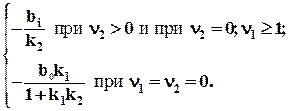 (48)

В этом случае ошибка ε_fуст может быть уменьшена путем увеличения коэффициента усиления k₂, что приводит к увеличению коэффициента усиления всей системы k=k₁ k₂.

Понятие об инвариантных системах

В предыдущем параграфе этой главы рассматривался вопрос о вычислении установившейся ошибки системы при известном законе изменения внешних воздействий. Зная, от каких факторов зависит ошибка, можно наметить пути обеспечения заданной точности системы.

Однако в целом ряде случаев законы изменения сигналов v(t) и f(t) оказываются неизвестными и фактически мы даже не располагаем никакой априорной информацией об этих воздействиях, в том числе и статиcтического характера, кроме информации о том, что эти сигналы существуют и приложены к определенным точкам структурной схемы.

При этом возникает задача создания системы, которая была бы нечувствительна к возмущениям произвольного вида и воспроизводила без искажения входной сигнал произвольного вида. Теория инвариантности как раз и рассматривает методы решения поставленной задачи.

Основным понятием теории инвариантности является понятие абсолютно инвариантной системы. Системой, абсолютно инвариантной к задающему воздействию v(t), называется система, имеющая нулевую установившуюся ошибку воспроизведения ε_уст( t) при любом законе изменения v(t). Системой, абсолютно инвариантной к возмущению f(t), называется система, имеющая нулевую установившуюся ошибку по возмущению ε _fyст(t) при любом законе изменения f(t). Учитывая существующие выражения для изображений этих ошибок

ε(р)=Ф_ε(р)v(p) и ε_f(p)=-Ф_f(p)f(p),

нетрудно установить, что условия абсолютной инвариантности сводятся к требованию равенства нулю передаточных функций по ошибке Ф_ε(р) и по возмущению Ф_f(p), т.е.

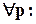Ф_ε(р)=0, Ф_f(p)=0. (49)

Рассмотрим условия физической осуществимости абсолютно инвариантных систем. Вопрос об этих условиях, возникающий при проектировании инвариантных систем, весьма важен.

Необходимое условие физической осуществимости заключается в выполнении системой условий инвариантности (49) как в замкнутом, так и в разомкнутом состоянии, другими словами, абсолютно инвариантная система не должна терять своих свойств при отключении обратной связи. Для обеспечения необходимого условия в системы вводятся дополнительные связи по возмущению и по входному сигналу. При этом возникает потребность в удовлетворении достаточного условия.

Достаточным условием физической осуществимости абсолютно инвариантных систем является физическая реализуемость дополнительно вводимых в систему элементов. Порядок знаменателя передаточной функции физически реализуемых элементов превышает (в крайнем случае, равен) порядок числителя этой же функции.

Обычно построить абсолютно инвариантную систему оказывается затруднительным. Поэтому на практике используют селективные абсолютно инвариантные системы, которые позволяют обеспечить нулевую установившуюся ошибку при некоторых определенных видах внешних воздействий. Условие абсолютной селективной инвариантности к задающему воздействию, изменяющемуся по известному закону v(t), выглядит следующим образом:

v(t): ε_уст(t)=0. (50)

Фактически условие селективной абсолютной инвариантности заключается в требовании равенства нулю нескольких первых коэффициентов ошибок системы или, другими словами, в требовании определенного порядка астатизма системы, как это имеет место, если v(t) является степенной функцией или полиномом.

Поэтому коэффициенты ошибок называют также коэффициентами инвариантности системы.

Селективная абсолютная инвариантность к задающему воздействию в системах с единичной обратной связью. Принцип внутренней модели.

Рассмотрим систему с единичной обратной связью, т.е. систему, в которой используется принцип управления по ошибке.

Пусть задающему воздействию v(t) соответствует изображение

v(p)=K_v(p)/D_v(p) (51)

и известны полюсы 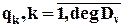этого изображения, другими словами, корни уравнения

D_v(p)=0,

Причем степень полинома D_v(p) равна degD_v. Тогда условие селективной абсолютной инвариантности

v(t): ε_уст(t)=0

можно записать по отношению к передаточной функции разомкнутой системы в виде

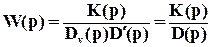, (52)

где D(p)= .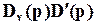

При этом передаточная функция по ошибке оказывается равной

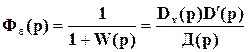, (53)

где Д(р)=D(p)+К(р) есть характеристический многочлен замкнутой системы управления (знаменатель передаточной функции Ф(р)), и ε_уст=0. Действительно, с учетом ε(p)=Ф_ε(р)v(p), (51) v(p)=K_v(p)/D_v(p) и (53) изображение ошибки

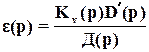
содержит лишь полюсы проектируемой системы р_i, i= , т.е. корни уравнения Д(р)=0, degД=n, которые для обеспечения устойчивости должны быть левыми. Следовательно, ошибка воспроизведения при простых корнях р_i , определяемая выражением

,

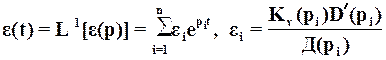с течением времени стремится к нулю, т.е.

.

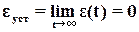Вывод. Передаточная функция W₂(p) управляющего устройства, обеспечивающего селективную абсолютную инвариантность системы управления к задающему воздействию, должна включать как свои полюсы все полюсы изображения этого задающего воздействия. Приведенный вывод можно рассматривать как конкретизацию принципа внутренней модели, который говорит о том, что хорошая система должна содержать модель внешней среды, в данном случае передаточная функция разомкнутой системы должна включать в себя математическую модель задающего воздействия, точнее знаменатель D_v(p) изображения по Лапласу задающего воздействия.

Из этого вывода следует, что условие селективной абсолютной инвариантности можно записать как .

Пример 1. Пусть задающее воздействие – постоянный сигнал v(t)=a₀, так что V(p)=a₀/p, q₁=0, и условие селективной абсолютной инвариантности принимает вид: W(0)=∞, т.е. значение АЧХ разомкнутой системы на нулевой частоте должно быть равно бесконечности, другими словами, ПФ разомкнутой системы должна включать в себя хотя бы одно интегрирующее звено – система должна обладать астатическими свойствами.

Пример 2. Пусть задающее воздействие – гармонический сигнал v(t)=v₀sinw_vt, с амплитудой v₀ и частотой w_v. Тогда V(p)=v₀w_v / (p²+w²_v), q_1,2=±jw_v. При этом условие селективной абсолютной инвариантности принимает вид: W(jw_v)=∞, т.е. значение АЧХ разомкнутой системы на частоте задающего воздействия |W(jw_v)| должно быть равно бесконечности, другими словами, знаменатель ПФ разомкнутой системы должен содержать сомножитель p²+w²_v.

Заметим, что в селективной абсолютной инвариантной системе с единичной обратной связью нулевая установившаяся ошибка воспроизведения сохраняется независимо от уровня задающего воздействия, а также от параметров объекта управления. Дело в том, что условие инвариантности (52) 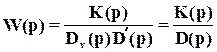, записанное применительно к передаточной функции разомкнутой системы, не зависит от передаточной функции объекта управления. При этом, как говорят, свойство селективной абсолютной инвариантности робастно.

Селективная инвариантность до ε к задающему воздействию.

Под селективной инвариантностью до ε понимается ограниченность установившейся ошибки воспроизведения задающих воздействий v(t) определенного вида. При такой форме инвариантности имеет место условие

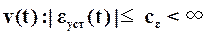(54)

где 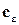- некоторая постоянная.

Селективная инвариантность до ε к гармоническому задающему воздействию.

Для задающих воздействий, изображения которых содержат лишь простые полюсы q_k, условие селективной инвариантности до ε можно записать в виде

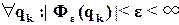. (55)

Гармоническое задающее воздействие

v(t)=v₀sin _vt

с изображением

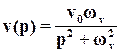
и полюсами q_1,2=±j _v как раз относится к таким воздействиям, поэтому условие (55) для гармонического задающего воздействия можно записать так:

. (56)

При этом мы учитываем, что в силу комплексной сопряженности выражени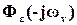й и 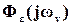, имеет место равенство ||=||.

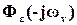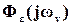Входящая в выражение (56) характеристика 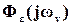представляет собой АФХ для ошибки, которая определяется как

,

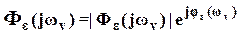где |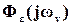| - АЧХ для ошибки, 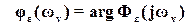- ФЧХ для ошибки.

Как видим, условие селективной инвариантности до ε по отношению к гармоническому задающему воздействию выполняется, если значение АЧХ для ошибки ограничено на частоте задающего воздействия.

В соответствии с физическим смыслом любой АЧХ звена (системы) АЧХ для ошибки определяет амплитуду ε₀ установившейся ошибки воспроизведения

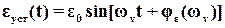
гармонического задающего воздействия (21), причем

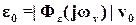. (57)

Следовательно, при выполнении условия (57) амплитуда установившейся ошибки воспроизведения и отсюда сама установившаяся ошибка воспроизведения ограничены, т.е.

.

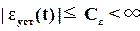Дата добавления: 2014-01-07