
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вращение твердого тела, имеющего плоскость материальной симметрии, вокруг неподвижной оси, перпендикулярной к этой плоскости
|
|
|
|
В этом случае неподвижная ось вращения тела является главной осью инерции тела в точке О. Каждой точке 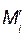 (рис. 224, а) соответствует точка
(рис. 224, а) соответствует точка  такой же массы, симметричная относительно заданной плоскости (на рис. 224, а эта плоскость заштрихована).
такой же массы, симметричная относительно заданной плоскости (на рис. 224, а эта плоскость заштрихована).
Из кинематики известно, что ускорения всех точек, лежащих на одной прямой, параллельной оси вращения, геометрически равны.
Поэтому силы инерции 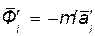 и
и 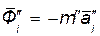 точек
точек 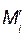 и
и  геометрически равны и их равнодействующая приложена в точке
геометрически равны и их равнодействующая приложена в точке  , лежащей в плоскости симметрии.
, лежащей в плоскости симметрии.
Отсюда следует, что в точке  приложена равнодействующая сил инерции всех точек тела, лежащих на перпендикуляре к плоскости симметрии, восстановленном в этой точке. Таким образом, сложение сил инерции точек тела в этом случае вращения сводится к сложению сил инерции точек материальной плоской фигуры, имеющей массу данного тела и тот же момент инерции относительно оси вращения (рис. 224, б).
приложена равнодействующая сил инерции всех точек тела, лежащих на перпендикуляре к плоскости симметрии, восстановленном в этой точке. Таким образом, сложение сил инерции точек тела в этом случае вращения сводится к сложению сил инерции точек материальной плоской фигуры, имеющей массу данного тела и тот же момент инерции относительно оси вращения (рис. 224, б).
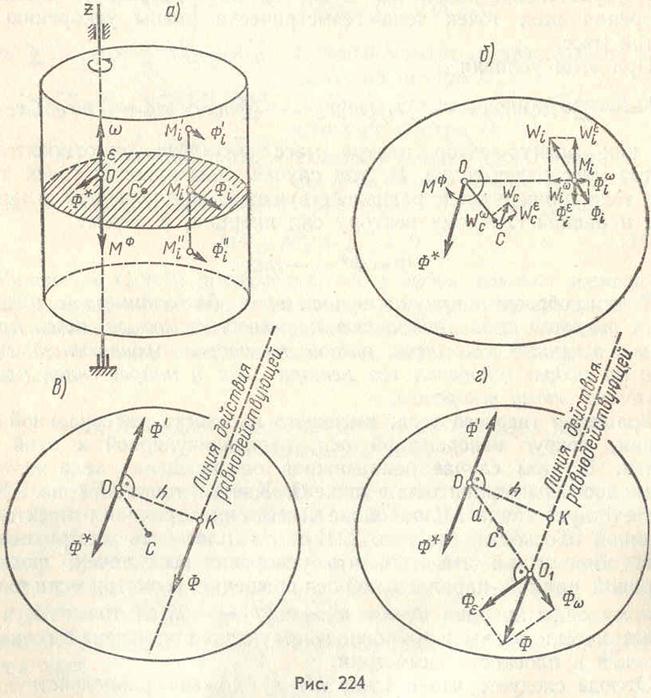
Приведем силы инерции точек фигуры к центру ее вращения О. При приведении получим силу, приложенную в этом центре, и пару сил, лежащую в плоскости фигуры. Сила равна главному вектору, определяемому формулой (109.3): 
Главный вектор направлен противоположно ускорению центра масс 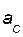 и имеет модуль:
и имеет модуль: 
Для определения момента пары разложим силу инерции каждой точки на вращательную и центробежную силу инерции, направленные противоположно вращательному и центростремительному ускорениям этой точки. Их модули определим по формулам:  и
и 
Так как линии действия центробежных сил инерции проходят через центр вращения О, то искомый момент пары равен сумме моментов вращательных сил инерции относительно точки О: 
Здесь  момент инерции материальной плоской фигуры относительно оси OZ, перпендикулярной к ее плоскости, равный моменту инерции данного тела относительно этой оси.
момент инерции материальной плоской фигуры относительно оси OZ, перпендикулярной к ее плоскости, равный моменту инерции данного тела относительно этой оси.
Таким образом, алгебраическая величина момента пары, составленной силами инерции,
 (109.4)
(109.4)
где Jz - момент инерции тела относительно оси вращения; ε — алгебраическая величина углового ускорения тела.
Вектор 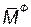 направлен перпендикулярно к плоскости фигуры, т. е. по оси вращения тела противоположно вектору углового ускорения:
направлен перпендикулярно к плоскости фигуры, т. е. по оси вращения тела противоположно вектору углового ускорения:
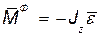
Как известно из статики (§ 29), силу 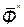 и пару с моментом
и пару с моментом 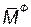 , лежащих в одной плоскости, можно заменить одной равнодействующей силой
, лежащих в одной плоскости, можно заменить одной равнодействующей силой  , геометрически равной главному вектору
, геометрически равной главному вектору 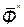 (рис. 224, в).
(рис. 224, в).
Линия действия этой силы отстоит от центра приведения О на расстоянии
 (109.5)
(109.5)
Таким образом, при вращении твердого тела, имеющего плоскость материальной симметрии, вокруг оси, перпендикулярной к этой плоскости, силы инерции точек тела приводятся к равнодействующей силе, лежащей в плоскости симметрии. Модуль и направление этой силы определяются формулой (109.3), а расстояние от ее линии действия до точки пересечения оси вращения с плоскостью симметрии - формулой (109.5).
Покажем, что линия действия равнодействующей сил инерции  проходит через центр качаний. Для этого продолжим линию действия этой силы до пересечения с прямой ОС; перенесем в точку их пересечения О1 силу
проходит через центр качаний. Для этого продолжим линию действия этой силы до пересечения с прямой ОС; перенесем в точку их пересечения О1 силу  и разложим ее на две составляющие
и разложим ее на две составляющие 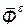 и
и  (рис. 224, г). На основании теоремы о моменте равнодействующей силы (ч. I, «Статика», § 29)
(рис. 224, г). На основании теоремы о моменте равнодействующей силы (ч. I, «Статика», § 29)
 (а)
(а)
Так как линия действия  проходит через точку О, то
проходит через точку О, то
 (б)
(б)
Принимая ОС = d, имеем 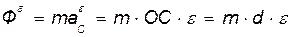
Поэтому на основании (а) и (б): 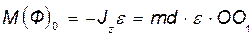 откуда
откуда 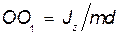
Из этого равенства на основании (81.3) следует, что точка О1 через которую проходит линия действия равнодействующей сил инерции  , является центром качаний.
, является центром качаний.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 641; Нарушение авторских прав?; Мы поможем в написании вашей работы!