Импульс силы характеризует передачу материальной точке механического движения со стороны действующих на нее тел за данный промежуток времени

Единицами импульса являются: в системе МКС импульс силы в один ньютон за время в одну секунду, т. е. один ньютон секунда (кг∙м/с), в системе СГС - одна дина∙секунда (г∙см/с), а в системе МКГСС—1 кгс∙с, в системе СИ: 1 Н∙сек.

Чтобы найти импульс переменной силы 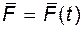за промежуток времени 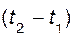, этот промежуток разбивают на п элементарных промежутков 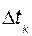и определяют элементарные импульсы силы за эти промежутки. Модуль элементарного импульса 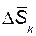равен произведению модуля силы в момент 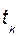на 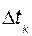, а направление совпадает с направлением силы в этот момент (рис. 107): 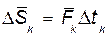(46.2)

Импульс силы 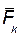за промежуток 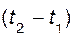определяется как предел геометрической суммы элементарных импульсов 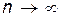при и при :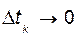

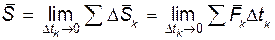
Предел векторной суммы бесчисленного множества бесконечно малых слагаемых 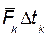при 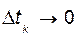называется векторным интегралом от вектора 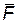по скалярному аргументу t. Таким образом, 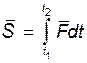(46.3)

Модуль и направление импульса переменной силы можно определить по способу проекций. Импульс 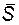переменной силы 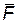за промежуток времени 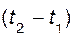представляет собой предел геометрической суммы элементарных импульсов 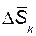. Поэтому проекция импульса 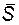на каждую координатную ось равна пределу алгебраической суммы проекций элементарных импульсов 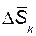на эту ось.

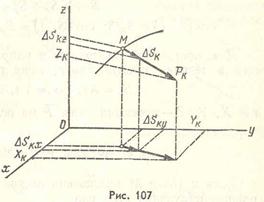
Проекции элементарного импульса 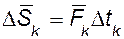на оси координат (рис. 107):

;

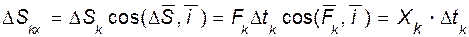аналогично

, ,

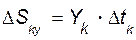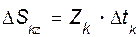где 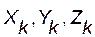- проекции силы 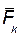на оси координат.

Просуммировав проекции элементарных импульсов и перейдя к пределу, получим определенные интегралы по переменной 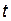, представляющие собой проекции импульса 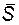на оси координат:

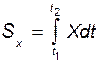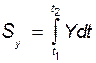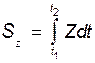, , . (46.4)

Здесь X = f₁(t); Y = f₂(t); Z = f₃(t) — проекции переменной силы 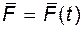на оси координат.

Модуль и направление импульса 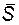определяются по его проекциям: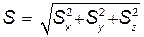

cos(S, i) = S_X/S; cos(S, j)=S_y/S; cos (S, k)=S_z/S. (46.5)

Для постоянной по модулю и направлению силы 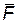, действующей в течение промежутка времени τ, формулы (46.4) имеют вид 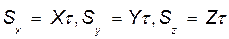, (46.6)

где X, Y, Z — проекции силы 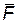на оси координат.

Покажем доказательство теоремы импульсов по методике профессора Фролова:

Умножим обе части уравнения № 5 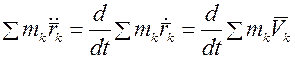на dt: 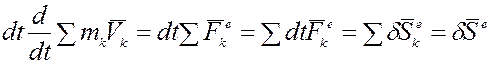или 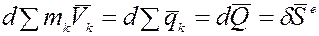окончательно:

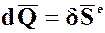, где

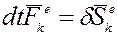- элементарный импульс k-той внешней силы, приложенный к материальной точке системы.

Импульс силы 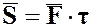характеризует передачу материальной точке, посредством приложенной к ней силы 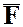, механического движения со стороны действующих на нее тел за данный промежуток времени 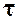. Направление вектора импульса силы 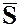совпадает с направлением приложенной к точке силы 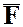, а его модуль равен произведению модуля силы на время ее действия .

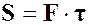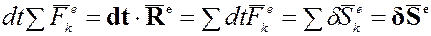или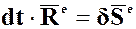

- элементарный импульс главного вектора внешних сил, приложенных к системе материальных точек;

Окончательно: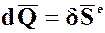

Теорема импульсов (механической системы):

Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме элементарных импульсов внешних сил, приложенных к системе, за тот же промежуток времени.

Или, после приведения системы сил к ее Главному вектору: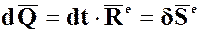

(Изменение количества движения механической системы за некоторый промежуток времени равно элементарному импульсу Главного вектора внешних сил, приложенных к системе, за тот же промежуток времени).

Дата добавления: 2014-01-07