Если Главный момент внешних сил относительно некоторой оси все время равен нулю, то кинетический момент механической системы относительно этой оси остается постоянным

Если линия действия Главного вектора внешних сил все время проходит через некоторый неподвижный центр, то кинетический момент механической системы относительно этого центра остается постоянным.

Если Главный момент внешних сил относительно некоторого центра все время остается равным нулю, то кинетический момент механической системы относительно этого центра остается постоянным.

Производная по времени от кинетического момента механической системы относительно некоторой оси равна Главному моменту внешних сил, действующих на эту систему, относительно этой оси.

Производная по времени от кинетического момента механической системы относительно некоторого центра геометрически равна Главному моменту внешних сил, действующих на эту систему, относительно этого же центра.

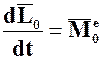(III)

Кинетический момент относительно произвольной оси (скалярная величина) равен проекции вектора кинетического момента относительно полюса, лежащего на этой оси. Тогда справедливо следующее соотношение между кинетическими моментами относительно оси и полюса для материальной точки:

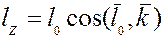
И для системы материальных точек:

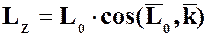
Момент количества движения материальной точки можно получить в аналитической форме разложением определителя векторного произведения: 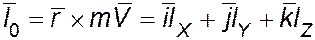, тогда определитель момента количества движения материальной точки: .

Разложим определитель на проекции по осям декартовых координат:

или

Векторному равенству (III) соответствуют три дифференциальных равенства в проекциях на оси координат:

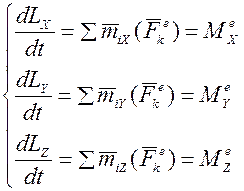, где 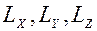кинетические моменты механической системы относительно осей координат, а 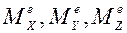главные моменты внешних сил относительно осей координат. Эти уравнения показывают, что:

Закон сохранения кинетического момента механической системы:

Закон состоит из двух следствий из теоремы:

Следствие 1:

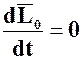Если то и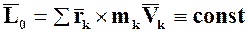

Это следствие можно выразить и в такой форме:

Следствие 2:

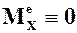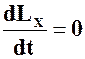Если то и

Кинематической интерпретацией теоремы об изменении кинетического момента механической системы относительно центра является

Теорема Резаля:

Скорость конца вектора кинетического момента механической системы относительно некоторого центра геометрически равна Главному моменту внешних сил, действующих на эту систему относительно того же центра.

Дата добавления: 2014-01-07