Изображение работы в виде площади

Установлено, что работа переменной силы на конечном перемещении M₁M₂ определяется криволинейным интегралом, взятым вдоль дуги М₁М₂ траектории, которую описывает точка приложения силы.

Криволинейный интеграл, определяющий работу силы, вычисляется обычно аналитически с помощью формулы (60.11) или графически — на основе формулы (60.9)

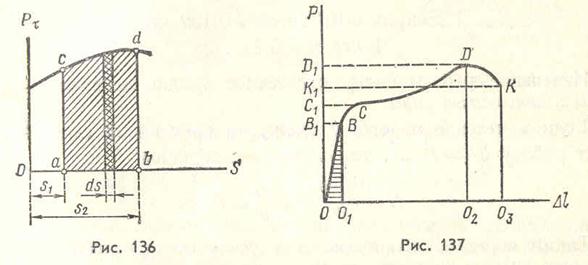
Для графического определения работы силы на перемещении М₁М₂ (рис. 131) используется график (рис. 136). По оси абсцисс этого графика отложены значения дуговой координаты точки S, a по оси ординат – соответствующие значения проекции силы на касательную . Построенная кривая изображает зависимость от S. Элементарная работа силы согласно (60.4)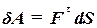

На рис. 136 эта величина изображается площадью элементарного прямоугольника, имеющего основание ds и высоту (Р_τ). Работа силы (Р) на перемещении М₁М₂ изобразится площадью фигуры acdb, ограниченной осью абсцисс, кривой 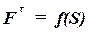и ординатами ас и bd, соответствующими точкам М₁ и М₂: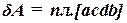

Если проекция силы на касательную отрицательна, то соответствующая площадь расположится ниже оси абсцисс, и работа силы будет отрицательна.

Для примера рассмотрим проводимое в механических лабораториях графическое вычисление работы, затрачиваемой на разрыв образца.

На рис. 137 изображена полученная опытным путем диаграмма растяжения образца. По оси ординат отложена величина растягивающей силы, а по оси абсцисс — производимое ею абсолютное удлинение образца, т. е. перемещение точки приложения силы. Точка В обозначает предел пропорциональности, С - предел текучести, D - наибольшую величину нагрузки, воспринимаемой образцом, К - нагрузку в момент разрыва образца.

Работа, затрачиваемая на растяжение образца до предела про порциональности, определяется площадью треугольника ОВО₁.

Площадь OBCDKO₃ определяет всю работу, затрачиваемую на разрыв испытуемого образца. Величину этой площади находят обычно при помощи планиметра или путем вычислений.

За единицу работы в системе МКС (СИ) принимается 1 джоуль (Дж), т. е. работа силы, равной 1 Н (ньютон) на перемещении в 1 м по направлению силы; в системе СГС—1 эрг, т. е. работа силы, равной 1 дин на перемещении в 1 см по направлению силы; в системе МКГСС за единицу работы принимается 1 кгс∙м, т. е. работа силы, равной 1 кгс на перемещении в 1 м по направлению силы.

1 джоуль = 10⁷ эргов = 0,102 кгс∙м; 1 кгс∙м = 9,81 Дж.

Изменение работы силы, отнесенное к единице времени, называется мощностью силы.

Если в течение малого промежутка времени dt сила совершает работу 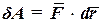то мощность этой силы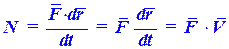

Таким образом, мощность силы равна скалярному произведению векторов силы и скорости ее точки приложения.

Аналитическое выражение мощности силы имеет вид 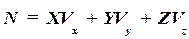, (60.13) где 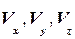-проекции скорости точки приложения силы на оси координат, а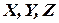- проекции силы на оси координат.

Из формулы (60.12) 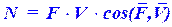(60.14)

Если направления силы Р и скорости v совпадают, то (60.15)

За единицу мощности в системе СИ (МКС) принимается 1 ватт (Вт) = 1 Дж/с = 0,102 кгс∙м/с, а в системе СГС—1 эрг/с. В системе МКГСС за единицу мощности принимается 1 кгс∙м/с.

Кроме того, применяются следующие единицы мощности: 1 киловатт (кВт)=10³Вт = 102 кгс∙м/с =1,36лошадиной силы; 1 лошадиная сила (HP) = 75 кгс∙м/с =736 Вт.

В технике часто за единицу работы принимается 1 киловатт∙час (кВт∙ч), т. е. работа, совершаемая в течение одного часа движущей силой машины, мощность которой равна 1 киловатту; 1 киловатт∙час = 1000 ∙ 3600 ватт∙секунд = 36 ∙ 10⁵ джоулей.

Вопросы для самоконтроля

1. Каковы две меры механического движения и соответствующие им измерители действия силы?

2. Как определяется работа постоянной по модулю и направлению силы на прямолинейном перемещении?

3. Чему равна работа силы трения скольжения, если эта сила постоянна по модулю и направлению?

4. Каким простым способом можно вычислить работу постоянной по модулю и направлению силы на криволинейном перемещении?

5 Чему равна работа равнодействующей силы?

6. Как выразить элементарную работу силы через элементарный путь точки приложения силы и как - через приращение дуговой координаты этой точки?

7. Каково векторное выражение элементарной работы?

8. Каково выражение элементарной работы силы через проекции силы на оси координат?

9. Напишите различные виды криволинейного интеграла_; определяющего работу переменной силы на конечном криволинейном перемещении.

10. В чем состоит графический способ определения работы переменной силы на криволинейном перемещении?

11. Как вычисляется работа силы тяжести и работа силы упругости?

12. На каких перемещениях работа силы тяжести:

а) положительна,

б) отрицательна,

в) равна нулю?

13. В каком случае работа силы упругости положительна и в каком - отрицательна?

14. Сформулируйте теорему об изменении кинетической энергии материальной точки.

15. Сформулируйте теорему об изменении кинетической энергии материальной точки в относительном движении. Почему равна нулю работа кориолисовой силы инерции?

16. Какова сумма работ внутренних сил твердого тела на любом перемещении тела?

17. Как вычисляется сумма элементарных работ внешних сил, приложенных к твердому телу:

а) в случае поступательного движения,

б) в случае его вращения вокруг неподвижной оси,

в) в общем случае его движения?

18)Как вычисляется мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси с угловой скоростью ω?

19. Что представляет собой сопротивление качению, что называется коэффициентом трения качения и какова его размерность?

20. Сформулируйте теорему Кенига о кинетической энергии механической системы в общем случае ее движения.

21. Как вычисляется кинетическая энергия твердого тела в различных случаях его движения?

22. Сформулируйте теорему об изменении кинетической энергии механической системы.

Дата добавления: 2014-01-07