Рассмотрим основные свойства силовой функции

Вычислим элементарную работу сил поля:

Пользуясь формулами (72.1), получаем:

т.е: (72.3)

Как видно, в том случае, если силовое поле является потенциальным, элементарная работа сил в этом поле равна полному дифференциалу силовой функции.

Работа сил поля на конечном перемещении механической системы из положения [1] в положение [2] (72.4) т. е. работа сил, действующих на точки механической системы в потенциальном поле, равна разности значений силовой функции в конечном и начальном положениях системы и не зависит от формы траекторий точек этой системы.

Формула (72.4) показывает, что работа сил, действующих на точки системы в потенциальном поле на всяком замкнутом перемещении, т. е. на перемещении, при котором начальные и конечные положения для всех точек совмещены, равна нулю, так как в этом случае U₂=U₁.

Введем понятие потенциальной энергии. Пусть, например, механическая система М₁ М₂,...,М_n (рис. 162) находится в потенциальном поле под действием сил Р₁ Р₂,..., Р_n. Примем некоторое произвольное положение этой системы за нулевое положение.

Потенциальная энергия системы в любом данном ее положении равна сумме работ сил потенциального поля, приложенных к ее точкам на перемещении системы из данного положения в нулевое.

Так как эта сумма работ зависит только от того, из какого положения система перемещается в выбранное нулевое положение, то потенциальная энергия П зависит только от положения системы.

Таким образом, потенциальную энергию системы можно представить как функцию координат ее точек: 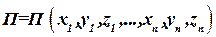(72.5)

Из определения потенциальной энергии следует, что в нулевом положении ее значение равно нулю:

Предположим, что механическая система перемещается из первого положения во второе .

Из определения потенциальной энергии следует, что работа сил поля, приложенных к точкам системы, на ее перемещении из первого положения в нулевое , равна потенциальной энергии системы в первом положении П₁. Аналогично работа сил поля на перемещении системы из второго положения в нулевое равна потенциальной энергии системы во втором положении П₂. Отсюда следует, что работа сил поля на перемещении системы из первого положения во второе (рис. 163) равна разности: (72.6)

Таким образом, работа сил, приложенных к точкам механической системы, на любом ее перемещении равна разности значений потенциальной энергии в начальном и конечном положениях системы.

Установим зависимость между силовой функцией и потенциальной энергией механической системы.

При перемещении механической системы из данного положения М₁ М₂,..., М_n в нулевое положение работа приложенных к точкам сил равна потенциальной энергии П системы в этом положении. С другой стороны, эту работу можно определить по формуле (72.4) как разность силовой функции U в нулевом положении и в данном, т.е. 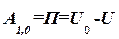(72.7)

Равенство (72.7) показывает, что потенциальная энергия системы П отличается от силовой функции U, взятой со знаком минус, на постоянную величину U_o. Из равенства (72.7)

, ,

Тогда на основании формулы (72.2) , , (72.8)

т. е. проекции на координатные оси силы, действующей в потенциальном поле на каждую точку M_i механической системы, равны взятым со знаком минус частным производным от потенциальной энергии системы по соответствующим координатам этой точки.

Рассмотрим, какой вид получат выведенные выше формулы при движении в потенциальном поле лишь одной материальной точки.

Силовая функция в этом случае имеет вид

U = U(x, у, z), (72.9)

где х, у, z —координаты рассматриваемой точки. Потенциальная энергия точки П = П(х, у, г). (72.10)

Формулы (72.1), определяющие проекции на оси координат силы поля, действующей на точку, принимают вид 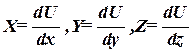(72.11)

(72.8) принимают вид , , (72.12)

Если применить понятие вектора-градиента от скалярной функции U

где - единичные векторы, направленные по осям координат, то силу 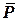можно выразить как градиент силовой функции U:

Очевидно, также, что

Из равенств (72.12) следует: (72.13)

Вследствие независимости смешанной производной от порядка дифференцирования имеем:

(72.14)

Соотношения (72.14) устанавливают необходимые условия, при выполнении которых силовое поле является потенциальным. Можно доказать и достаточность этих условий.

Следует отметить, что в выражение потенциальной энергии П (х, у, z) можно включить любую добавочную постоянную величину, так как от этого частные производные от потенциальной энергии не изменятся.

Постоянные по величине и направлению силы могут быть отнесены к силам, имеющим потенциал. Так, например, постоянная по величине сила 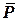, параллельная оси Оz и совпадающая с ней по направлению, имеет проекцию только на эту ось Z = P, так как ее проекции на оси Ох и Оy равняются нулю. Поэтому и

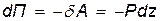
Потенциальная энергия П в этом случае определяется выражением

Рассмотрим два примера на применение соотношений (72.14) к выяснению вопроса о том, является ли рассматриваемое силовое поле потенциальным.

Сначала рассмотрим двухмерное силовое поле центральной силы, произвольным образом зависящей от расстояния до центра (рис. 164, а).

; ,

где ; ; Тогда

Так как в этом силовом поле — то это поле консервативно.

Теперь рассмотрим двухмерное силовое поле, в котором на находящуюся в нем точку действует сила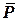, перпендикулярная к радиусу-вектору точки. Модуль силы 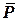не зависит от положения точки. Пусть силы 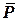, образующие поле, ориентированы таким образом, что создают относительно начала координат положительный момент (рис. 164, б).

В этом силовом поле имеем:

, ,

,

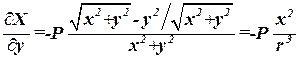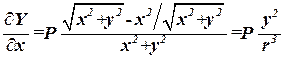
Так как в этом случае , то

рассматриваемое силовое поле неконсервативно.

По заданной функции П = (х, у, z) (72.10) легко дать геометрическую характеристику зависимости потенциальной энергии точки от ее положения в пространстве. Геометрическое место точек пространства, в которых потенциальная энергия материальной точки имеет одно и то же значение, определяется из уравнения

П(х, у, z) = С. (72.15)

Уравнение (72.15) определяет некоторую поверхность в пространстве, которая называется поверхностью равного потенциала или эквипотенциальной поверхностью. Давая параметру С всевозможные близкие значения, можно получить бесчисленное множество эквипотенциальных поверхностей, разделяющих поле на тонкие слои. Через каждую точку поля проходит одна эквипотенциальная поверхность.

Параметру С = 0 соответствует нулевая эквипотенциальная поверхность, проходящая через нулевое положение М^(о); во всех ее точках потенциальная энергия равна нулю.

Установим направление силы поля в каждой точке по отношению к эквипотенциальной поверхности, проходящей через эту точку.
Предположим, что точка М перемещается в бесконечно близкое положение М' на той же эквипотенциальной поверхности (рис. 165).

Тогда элементарная работа силы поля Р на перемещении ММ' согласно (60.5)

С другой стороны, эта работа определяется формулой (72.6):

,

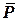потому что П = П' в точках М и М', принадлежащих одной и той же эквипотенциальной поверхности. Так как Р≠О, ММ'≠0, то , т. e. , следовательно, сила направлена по нормали к эквипотенциальной поверхности, проходящей через данную точку.

Допустим, что точка получает элементарное перемещение ММ" по направлению силы. Тогда

Согласно формуле (72.6)

Сопоставляем эти два выражения элементарной работы: или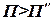

Следовательно, сила 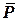направлена в сторону уменьшения значений потенциальной энергии.

Дата добавления: 2014-01-07