Примеры потенциальных силовых полей

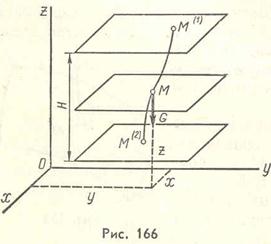Поле силы тяжести. Сила тяжести, работа которой не зависит от траектории ее точки приложения, является примером силы, имеющей потенциал. Исследуем поле этой силы:

1. Рассмотрим сначала движение в этом поле одной материальной точки. Направим ось Z вверх по вертикали, а оси X и Y произвольно в горизонтальной плоскости.

Определим потенциальную энергию материальной точки М (рис. 166), применяя формулу (72.12) к проекциям силы тяжести G на оси координат:

, ,

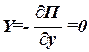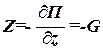
Отсюда следует, что потенциальная энергия точки П зависит только от координаты Z.

Тогда 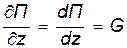, откуда

Интегрируя, получаем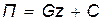

Предположим, что потенциальная энергия точки равна нулю при z = 0, т. е. примем за нулевую эквипотенциальную поверхность координатную плоскость хОу.

Тогда С=0 и потенциальная энергия точки

П = Gz. (73.1)

Согласно (72.13), уравнения эквипотенциальных поверхностей имеют вид

Gz = const или z = const,

т. е. эквипотенциальные поверхности поля силы тяжести представляют собой горизонтальные плоскости.

Очевидно, что эквипотенциальные поверхности поля силы тяжести можно считать плоскостями лишь на сравнительно небольшом протяжении, где можно пренебрегать кривизной земной поверхности.

Сила тяжести направлена перпендикулярно к этим плоскостям в сторону уменьшения значений потенциальной энергии.

Определим работу силы тяжести на перемещении точки из М⁽¹⁾ в M⁽²⁾ по формуле (72.6):

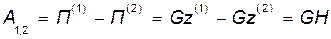
где 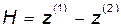при .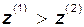

Полученное выражение совпадает с формулой (61.1).

2. Рассмотрим теперь механическую систему М₁, М₂,..., М_n, на которую действуют силы тяжести G₁,G₂,..., G_n (рис. 167).

Определим потенциальную энергию системы при помощи формулы (73.1):

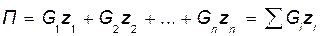
Координаты центра тяжести системы определяются по формулам из статики:

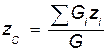, откуда 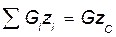, тогда 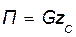(73.2)

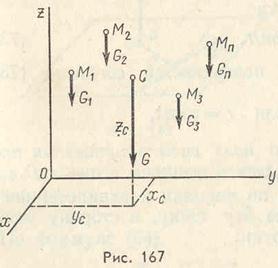
т. е. потенциальная энергия механической системы, находящейся под действием сил тяжести, равна произведению веса системы на высоту ее центра тяжести над нулевой эквипотенциальной плоскостью.

Дата добавления: 2014-01-07