Малые свободные колебания системы с двумя степенями свободы

Лекция 11.

Тема №5. Механические колебания. Удар.

Колебания системы с несколькими степенями свободы, имеющие важные практические приложения, отличаются от колебаний системы с одной степенью свободы рядом существенных особенностей. Чтобы дать представление об этих особенностях, рассмотрим случай свободных колебаний системы с двумя степенями свободы.

Пусть положение системы определяется обобщенными координатами
q ₁ = q ₂ и при q ₁ = q ₂ = 0 система находится в устойчивом равновесии. Тогда кинетическую и потенциальную энергии системы, с точностью до квадратов малых величин можно найти так же, как были найдены равенства (3), (4), и представить в виде:

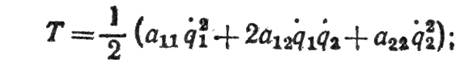(9)

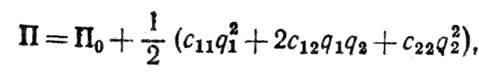(10)

где инерционные коэффициенты a ₁₁, a ₁₂, a ₂₂ И квазиупругие коэффициенты c ₁₁, c ₁₂, c ₂₂ — величины постоянные. Если воспользоваться двумя уравнениями Лагранжа вида (2) и подставить в них эти значения Т и П, то получим следующие дифференциальные уравнения малых колебаний системы с двумя степенями свободы

(11)

Будем искать решение уравнений (11) в виде:

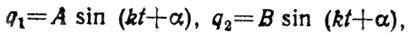(12)

где А, В, k, a — постоянные величины. Подставив эти значения q₁ , q₂ в уравнения (145) и сократив на sin (kt + а), получим

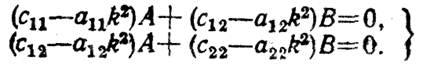(13)

Чтобы уравнения (13) давали для А и В решения, отличные от нуля, определитель этой системы должен быть равен нулю или, иначе, коэффициенты при А я В в уравнениях Должны быть пропорциональны, т. е.

(14)

Отсюда для определения А получаем следующее уравнение, называемое уравнением частот:

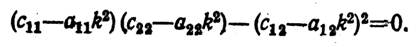(15)

Корни 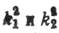этого уравнения вещественны и положительны; это доказывается мА тематически, но может быть обосновано и тем, что иначе

не будут вещественны и уравнения (11) не будут иметь решений вида (12), чего для системы, находящейся в устойчивом равновесии, быть не может (после возмущений она должна двигаться вблизи положения
q₁ = q₂ = 0).

Определив из (15) k₁ и k₂ , найдем две совокупности частных решений вида (12). Если учесть, что согласно (14) В = п А, эти решения будут:

(16)

(17)

где n₁ и n₂ — значения, которые я получает из (148) при k = k₁ и k = k ₂ соответственно.

Колебания, определяемые уравнениями (16) и (17), называются главными колебаниями, а «х частоты k₁ и k₂ — собственными частотами системы. При этом, колебание с частотой k₁ (всегда меньшей) называют первым главным колебанием, • с частотой k₂ — вторым главным колебанием. Числа n₁ и n₂, определяющие отношения амплитуд (или самих координат, т. е. q₂ / q₁ ) в каждом из этих колебаний, называют коэффициентами формы.

Так как уравнения (11) являются линейными, то суммы частных решений (16) и (17) тоже будут решениями этих уравнений:

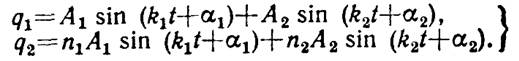(18)

Равенства (18), содержащие четыре произвольных постоянных A₁ , A₂ , a ₁, a ₂ , определяемых по начальным условиям, дают общее решение уравнений (11) и определяют закон малых колебаний системы. Эти колебания слагаются из двух главных колебаний с частотами k₁ и k₂ и не являются гармоническими. В частных случаях, при соответствующих начальных условиях, система может совершать одно из главных колебаний (например, первое, если А₂ = 0) и колебание будет гармоническим.

Собственные частоты k₁ , k₂ и коэффициенты формы n₁ и n₂ , не зависят от начальных условий и являются основными характеристиками малых колебаний системы; решение конкретных задач обычно сводится к определению этих характеристик.

Сопоставляя результаты этого и предыдущего параграфов, можно получить представление о том, к чему сведется исследование затухающих и вынужденных колебаний системы с двумя степенями свободы. Мы этого рассматривать не будем, отметим лишь, что при вынужденных колебаниях резонанс у такой системы может возникать дважды: при p ≈ k₁ и при р ≈ k₂ (р — частота возмущающей силы). Наконец, отметим, что колебания системы с s степенями свободы будут слагаться из s колебаний с частотами
k₁ , k₂...k_S, которые должны определяться из уравнения степени s относительно k². Это связано со значительными математическими трудностями, преодолеть которые можно с помощью электронных вычислительных (или аналоговых) машин.

Задача 1.

Определить собственные частоты и коэффициенты формы малых колебаний двойного физического маятника, образованного стержнями 1 и 2 одинаковой массы т и длины l (рис. 1, а).

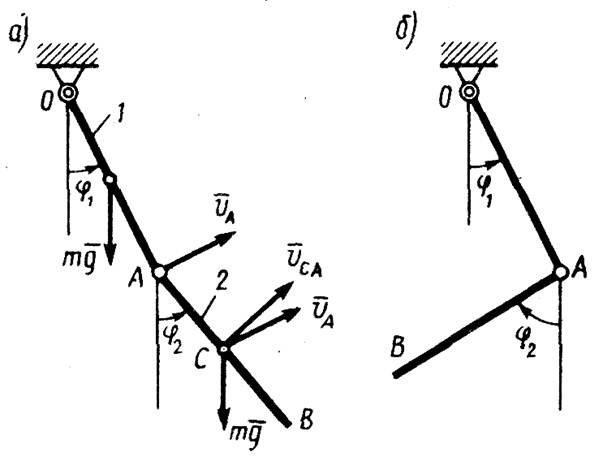
Рис. 1

Решение. Выберем в качестве обобщенных координат малые углы φ₁ и φ₂. Тогда

при требуемой точности подсчетов,

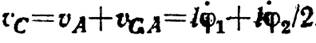
В итоге

Далее

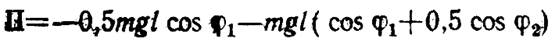
или, полагая

Из равенств (а) и (б) видно, каковы здесь значения a ₁₁, a ₁₂, a ₂₂ и
c ₂₂ (c ₁₂ = 0). При этих значениях коэффициентов уравнение частот (15) примет вид:

Его корнями будут:

откуда

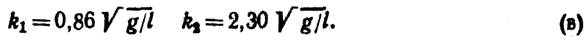
Подставляя теперь в любое из отношений, стоящих в левой части равенства (14), сначала k₁, а затем k₂ , получим

n₁ =1,43, n₂ = -2,10. (г)

Таким образом, при первом главном колебании оба стержня будут в каждый момент времени отклонены от вертикали в одну и ту же сторону (рис. 1, а) и φ₂/φ₁ = l,43, а при втором главном колебании — в разные стороны (рис, 1, б) и |φ₂/φ₁| = 2,10.

Дата добавления: 2014-01-07