Общие теоремы теории удара

Рассмотрим, какой вид принимают общие теоремы динамики для системы материальных точек при ударе.

1. Теорема об изменении количества движения системы при ударе. Уравнение об изменении количества движения, сохраняет свой вид и для случая удара. Но так как импульсами обычных сил при ударе пренебрегают, то в правой части останутся только ударные импульсы. Следовательно, при ударе:

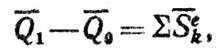(20)

т. е. изменение количества движения системы за время удара равно сумме всех внешних ударных импульсов, действующих на систему.

В проекциях на любую координатную ось х уравнение (20) дает:

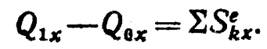(20’)

В дальнейшем будем ударный импульс обозначать просто символом S, так как импульсы неударных сил в теории удара не рассматриваются.

Если геометрическая сумма всех внешних ударных импульсов равна нулю, то, как видно из уравнения (20), количество движения системы за время удара не изменяется. Следовательно, внутренние ударные импульсы не могут изменить количества движения всей системы.

2. Теорема об изменении главного момента количеств движения системы (теорема моментов) при ударе. Теорема моментов принимает для случая удара вид, объясняется это тем, что точки системы за время удара не перемещаются. Рассмотрим систему, состоящую из п материальных точек. Обозначим равнодействующую внешних ударных импульсов, действующих на точку с массой m_k, через S^е_k, а равнодействующую действующих на ту же точку внутренних ударных импульсов — через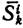

Тогда по уравнению (19) будет:

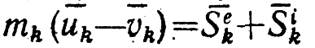
или

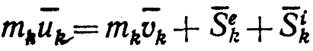
Входящие в это равенство векторы приложены к точке, которая, как. было указано, за время удара остается неподвижной. Тогда, беря моменты этих векторов относительно какого-нибудь центра О, по теореме Вариньона, справедливой для любых векторных величин, найдем, что

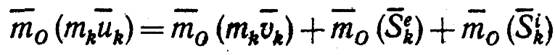
Составляя такие равенства для всех точек системы и складывая их почленно, получим:

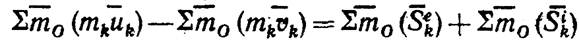
Суммы, стоящие слева, представляют собой главные моменты количеств движения системы относительно центра О в конце и в начале удара, которые обозначим K₁ и K₀. Стоящая справа сумма моментов внутренних ударных импульсов по свойству внутренних сил равна нулю. Окончательно находим

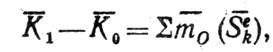(21)

т. е. изменение за время удара главного момента количеств движения системы относительно какого-нибудь центра равно сумме моментов относительно того же центра всех действующих на систему внешних ударных импульсов.

В проекциях на. любую ось х равенство (21) дает

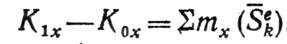(21)

Из полученных уравнений следует, что если сумма моментов внешних ударных импульсов относительно какого-нибудь центра (или оси) равна нулю, то главный момент количеств движения системы относительно этого центра (или оси) за время удара неизменяется. Следовательно, внутренние ударные импульсы не могут изменить главный момент количеств движения системы.

Дата добавления: 2014-01-07