Пример 1. Точка движется прямолинейно по закону S = t4 +2t (S - в метрах, t - в секундах)

Точка движется прямолинейно по закону S = t⁴ +2t (S - в метрах, t - в секундах). Найти ее среднее ускорение в промежутке между моментами t₁ = 5 с, t₂ = 7 с, а также ее истинное ускорение в момент t ₃ = 6 с.

Решение.

1. Находим скорость движения точки как производную от пути S по времени t, т.е.

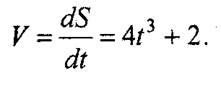
2. Подставляя вместо t его значения t₁ = 5 с и t₂ = 7 с, находим скорости:

V₁ = 4 • 5³ + 2 = 502 м/с; V₂ = 4 • 7³ + 2=1374 м/с.

3. Определяем приращение скорости ΔV за время Δt = 7 - 5 =2 с:

ΔV = V₂ - V₁ = 1374 - 502 = 872 м/с.

4. Таким образом, среднее ускорение точки будет равно

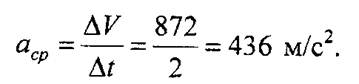
5. Для определения истинного значения ускорения точки берем производную скорости по времени:

6. Подставляя вместо t значение t₃ = 6 с, получим ускорение в этот момент времени

a_ср=12-6³=432 м/с².

Криволинейное движение. При криволинейном движении скорость точки изменяется по величине и направлению.

Представим себе точку М, которая за время Δt, двигаясь по какой-то криволинейной траектории, переместилась в положение М₁ (рис. 6).

Вектор приращения (изменения) скорости ΔV будет

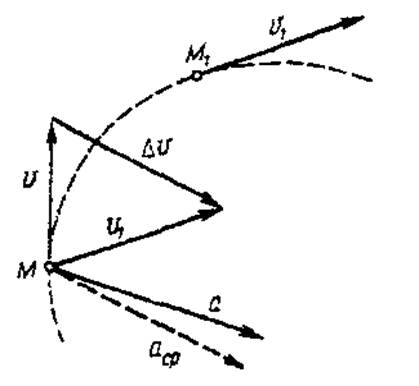
Рис. 6

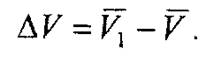
Для нахождения вектора ΔV перенесем вектор V₁, в точку М и построим треугольник скоростей. Определим вектор среднего ускорения:

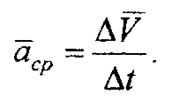
Вектор а_ср параллелен вектору ΔV, так как от деления вектора на скалярную величину направление вектора не изменяется. Вектор истинного ускорения есть предел, к которому стремится отношение вектора скорости к соответствующему промежутку времени Δt, стремящемуся к нулю, т.е.

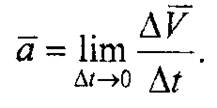
Такой предел называют векторной производной.

Таким образом, истинное ускорение точки при криволинейном движении равно векторной производной по скорости.

Из рис. 6 видно, что вектор ускорения при криволинейном движении всегда направлен в сторону вогнутости траектории.

Для удобства расчетов ускорение раскладывают на две составляющие к траектории движения: по касательной, называемое касательным (тангенциальным) ускорением а,, и по нормали, называемое нор-мальным ускорением а_n (рис. 7).

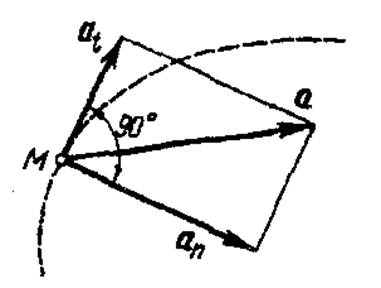
Рис. 7

В этом случае полное ускорение будет равно

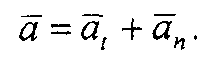
Касательное ускорение совпадает по направлению со скоростью точки или противоположно ей. Оно характеризует изменение величины скорости и соответственно определяется по формуле

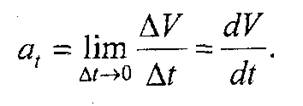
Нормальное ускорение перпендикулярно к направлению скорости точки, а численное значение его определяется по формуле

где r - радиус кривизны траектории в рассматриваемой точке.

Так как касательное и нормальные ускорения взаимно перпендикулярны, поэтому величина полного ускорения определяется по формуле

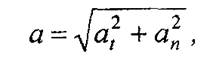
а направление его

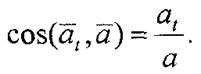
Если 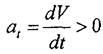, то векторы касательного ускорения и скорости направлены в одну сторону и движение будет ускоренным.

Если 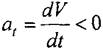, то вектор касательного ускорения направлен в сторону, противоположную вектору скорости, и движение будет замедленным.

Вектор нормального ускорения всегда направлен к центру кривизны, поэтому оно называется центростремительным.

Дата добавления: 2014-01-07