Пример 2

Точка обода маховика двигателя в период разгона движется согласно закону S = 0,2t³ (S - в метрах, t - в секундах). Радиус маховика r = 0,8 м. Определить касательное и нормальное ускорения точки в момент, когда ее скорость V = 20 м/с.

Решение.

1. Определяем время разгона маховика при скорости V = 20 м/с, для чего вычислим производную пути по времени, т.е.

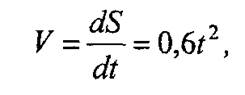
откуда время t будет

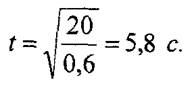
2. Для этого момента времени находим касательное ускорение как производную скорости по времени:

3. Находим нормальное ускорение в конце разгона маховика, т.е.

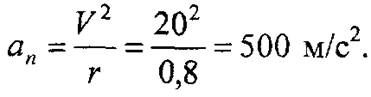
Анализируя приведенные формулы касательного и нормального ускорений, можно установить следующие виды движения точки (рис. 8).

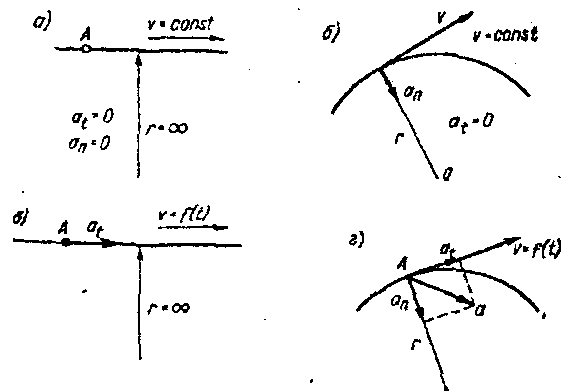
Рис. 8.

1. Равномерное прямолинейное движение (рис. 8, а). В

этом случае касательное ускорение равно нулю, так как величина скорости не изменяется (ΔV = 0) и нормальное ускорение равно нулю, так как r = ∞, т.е.

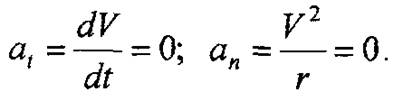
Значит и полное ускорение равно нулю: a = 0.

2. Равномерное криволинейное движение (рис. 8, б). Оно характеризуется тем, что численное значение скорости постоянно (V = const), а вектор скорости меняется (r ≠ ∞), т.е.

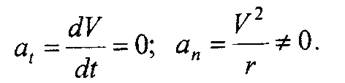
Полное ускорение при этом движении равно нормальному ускорению:

а =а_n

3. Неравномерное прямолинейное движение (рис. 27, в) характеризуется тем, что модуль скорости движения точки изменяется (ΔV ≠ 0), а радиус кривизны траектории движения точки равен бесконечности (r = со). В этом случае касательное ускорение не равно нулю, а нормальное равно нулю, т.е.

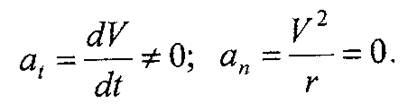
Полное ускорение в этом случае будет

а = а_t

4. Неравномерное криволинейное движение (рис. 27, г) характерно тем, что скорость движения непостоянна (V ≠ const) и вектор скорости изменяется (r ≠ ∞). В этом случае касательное и нормальное ускорения не равны нулю, т.е.

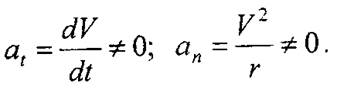
Полное ускорение складывается геометрически из касательного и нормального ускорений:

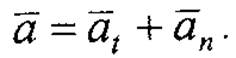
5. Равнопеременное движение точки характеризуется тем, что если нормальное ускорение не равно нулю (а_n ≠ 0), то имеет место криволинейное движение, а если а_n = 0 - прямолинейное. В этом случае касательное ускорение есть величина постоянная, т.е.

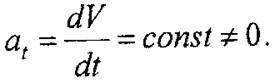
Формулы равнопеременного движения точки. Равнопеременное движение может быть равномерно ускоренным, если численное значение скорости увеличивается, и равномерно замедленным, если численное значение скорости уменьшается. Величину ускорения можно определить через значения скорости в начале и в конце произвольного промежутка времени t, т.е.

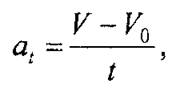
где V₀ - начальная скорость.

Преобразуя формулу касательного ускорения находим значение скорости:

V = V₀ + a_t, t.

При равномерно ускоренном движении ускорение а_t имеет положительное значение, а при равномерно замедленном - отрицательное.

Пусть, пройденный точкой при равнопеременном движении, определяется из уравнения:

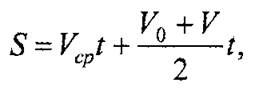
откуда после подстановки значения скорости и преобразований получим уравнение пройденного точкой пути, т.е.

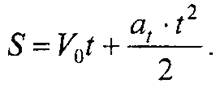
Дата добавления: 2014-01-07