
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
П. 3.3. Решение логических задач
|
|
|
|
Можно выделить следующую последовательность шагов в решении логических задач.
1. Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
2. Записать условие задачи на языке алгебры логики, соединить простые высказывания в сложные с помощью логических операций.
3. Составить единое логическое выражение для требований задачи.
4. Используя законы алгебры логики, попытаться упростить полученное выражение и вычислить все его значения либо построить таблицу истинности для рассматриваемого выражения.
5. Выбрать решение – набор значений простых высказываний, при котором построенное логическое выражение является истинным.
6. Проверить, удовлетворяет ли полученное решение условию задачи.
Пример:
Задача 1: «Пытаясь вспомнить победителей прошлогоднего турнира, пять бывших зрителей турнира заявили, что:
1. Антон был вторым, а Борис – пятым.
2. Виктор был вторым, а Денис – третьим.
3. Григорий был первым, а Борис – третьим.
4. Антон был третьим, а Евгений – шестым.
5. Виктор был третьим, а Евгений – четвертым.
Впоследствии выяснилось, что каждый зритель ошибся в одном из двух своих высказываний. Каково было истинное распределение мест в турнире».
Решение:
1) Обозначим через 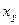 первую букву в имени участника турнира, а
первую букву в имени участника турнира, а 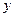 – номер места, которое он имеет, т.е. имеем
– номер места, которое он имеет, т.е. имеем  .
.
2) 1. 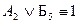 ; 3.
; 3. 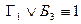 ; 5.
; 5.  .
.
2. 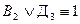 ; 4.
; 4.  .
.
3) Единое логическое выражение для всех требований задачи: 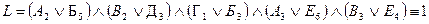 .
.
4) В формуле L проведем равносильные преобразования, получим: 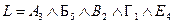 .
.
5) Из пункта 4 следует:  ,
, 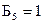 ,
,  ,
,  ,
,  .
.
6) Распределение мест в турнире: Антон был третьим, Борис – пятым, Виктор – вторым, Григорий – первым, а Евгений – четвертым.
Задача 2: «По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено:
1. если Иванов не виновен или Петров виновен, то Сидоров виновен;
2. если Иванов не виновен, то Сидоров не виновен.
Виновен ли Иванов?»
Решение:
1) Рассмотрим высказывания:
А: «Иванов виновен», В: «Петров виновен», С: «Сидоров виновен».
2) Факты, установленные следствием:  ,
,  .
.
3) Единое логическое выражение:  . Оно истинно.
. Оно истинно.
 . Составим для него таблицу истинности.
. Составим для него таблицу истинности.
| А | В | С | L |
Решить задачу – значит указать, при каких значениях А полученное сложное высказывание L истинно. Если  , а
, а 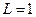 , то у следствия не достаточно фактов для того, чтобы обвинить Иванова в преступлении. Анализ таблицы показывает
, то у следствия не достаточно фактов для того, чтобы обвинить Иванова в преступлении. Анализ таблицы показывает  и
и 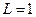 , т.е. Иванов в ограблении виновен.
, т.е. Иванов в ограблении виновен.
Вопросы и задания.
1. Составить РКС для формул:
а) 
б) 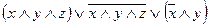
в) 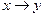
г) 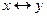
д) 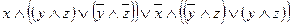
2. Упростить РКС:
а)
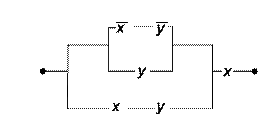
б)
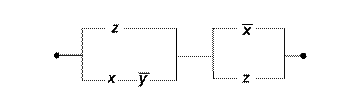
в)

3. По данной переключательной схеме построить соответствующую ей логическую формулу.
а)
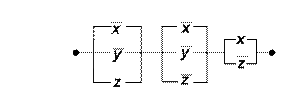
б)
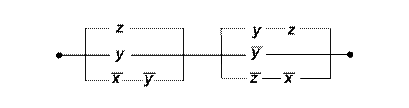
в)

г)

4. Проверить равносильность РКС:
а)
 и
и 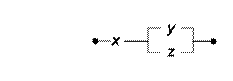
б)
 и
и 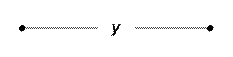
в)
 и
и
г)
 и
и
5. Построить схему из трех переключателей и лампочки таким образом, чтобы лампочка зажигалась только в том случае, когда ровно два переключателя находятся в положении «включено».
6. По данной таблице проводимости построить схему из функциональных элементов с тремя входами и одним выходом, реализующую формулу  .
.
| x | y | z | F |
7. Проанализируйте схему, приведенную на рисунке, и выпишите формулу для функции F.

8. Задача: «Однажды следователю пришлось одновременно допрашивать трех свидетелей: Клода, Жака, Дика. Их показания противоречили друг другу, и каждый из них обвинял кого-нибудь во лжи.
1) Клод утверждал, что Жак лжет.
2) Жак обвинял во лжи Дика.
3) Дик уговаривал следователя не верить ни Клоду, ни Жаку.
Но следователь быстро вывел их на чистую воду, не задав им ни одного вопроса. Кто из свидетелей говорил правду?
9. Определить, кто из четырех студентов сдал экзамен, если известно, что:
1) Если первый сдал, то и второй сдал.
2) Если второй сдал, то третий сдал или первый не сдал.
3) Если четвертый не сдал, то первый сдал, а третий не сдал.
4) Если четвертый сдал, то и первый сдал.
10. На вопрос, кто из трех студентов изучал логику, был получен ответ: если изучал первый, то изучал и третий, но не верно, что если изучал второй, то изучал и третий. Кто изучил логику?
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 6268; Нарушение авторских прав?; Мы поможем в написании вашей работы!