Підставивши одержаний вираз до рівняння

,

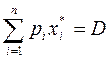маємо

.

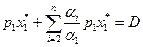Звідси

та

, .

ІІ Бінарні відношення R (множина впорядкованих пар меню споживання)

- множина припустимих меню (споживацьких наборів), R – відношення переваг споживача (відношення типу “не гірше”).

Треба знайти таке , що V 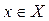виконується 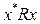. Для існування х^* необхідне виконання таких умов:

1. Повнота: V х⁽¹⁾, х⁽²⁾ має виконуватись або х⁽¹⁾ Rx⁽²⁾, або х⁽²⁾ Rx⁽¹⁾, або і те, і інше (тоді х⁽¹⁾ та х⁽²⁾ звуться еквівалентними, що позначається ). Відношення R є об’єднанням відношення еквівалентності та відношення строгої переваги .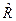

2. Рефлексивність: V х виконується .

3. Транзитивність: якщо для довільних х⁽¹⁾, х⁽²⁾, х⁽³⁾ виконується х⁽¹⁾ Rx⁽²⁾, х⁽²⁾ Rx⁽³⁾, то має також виконуватись х⁽¹⁾ Rx⁽³⁾.

4. Неперервність: для будь-яких меню споживання у та z множини { x: xRy } та { x: zRx } – замкнені.

Зауважимо, що перші 3 умови мають, передусім, економічний зміст. У той же час остання умова – здебільше математична (аналогія – неперервність функції корисності).

За зазначених умов існує індекс корисності – функція ν (х): х⁽¹⁾ Rx⁽²⁾ ↔ ν (х⁽¹⁾) ≥ ν (х⁽²⁾) та задача пошуку х^* еквівалентна оптимізаційній задачі

ν (х) → max,

(p, x) ≤ D,

x ≥ 0.

Тут спостерігається повна аналогія з кардинальним виміром корисності!

Дещо відмінною є ситуація, коли не виконуються раніш зроблені припущення щодо властивостей бінарного відношення R. Передусім, це стосується транзитивності. Переваги реальних споживачів вочевидь є рефлексивними, якщо ж відношення R не повне, його можна замінити відношенням R ₁: x ⁽¹⁾ R ₁ x ⁽²⁾ , якщо або x ⁽¹⁾ Rx ⁽²⁾ , або x ⁽¹⁾ та x ⁽²⁾ неможливо порівняти. Відношення R ₁ буде повним, а меню споживання x ⁽¹⁾ та x ⁽²⁾ , такі, що не виконується ані x ⁽¹⁾ Rx ⁽²⁾ , ані x ⁽²⁾ Rx ⁽¹⁾ , будуть еквівалентними за цим відношенням.

Невиконання умови транзитивності означає, що існують такі x ⁽¹⁾, x ⁽²⁾ , x ⁽³⁾, що 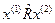, x ⁽²⁾ Rx ⁽³⁾, проте x ⁽³⁾ Rx ⁽¹⁾. За цих умов не існує індекса корисності, породженого R, бо ні для якої функції V(x) не можуть одночасно виконуватись нерівності

V (x ⁽¹⁾ ) > V (x ⁽²⁾ ), V (x ⁽²⁾ ) ≥ V (x ⁽³⁾ ), та V (x ⁽³⁾ ) ≥ V (x ⁽¹⁾ ).

Для формалізації нетранзитивних відношень потрібно застосовувати інший інструментарій, наприклад, індикатор переваг.

Індикатором переваг зветься така функція h (x ⁽¹⁾, x ⁽²⁾ ), що h (x ⁽¹⁾, x ⁽²⁾ ) > 0, коли ,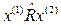

h (x ⁽¹⁾, x ⁽²⁾ ) < 0, коли ,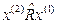

h (x ⁽¹⁾, x ⁽²⁾ ) = 0, коли .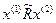

Очевидно, що таку функцію можна побудувати для будь-якого відношення R, поклавши, що вона дорівнює 1, 0, -1 для трьох раніше розглянутих випадків. Іноді нетранзитивні переваги вдається описати за допомогою неперервних індикаторів, наприклад, нехай x ⁽¹⁾ та x ⁽²⁾ - це дійсні числа, а функція h (x ⁽¹⁾, x ⁽²⁾ ) визначена наступним чином:

h (x ⁽¹⁾, x ⁽²⁾ ) = x ⁽¹⁾ x ⁽²⁾ (|x ⁽¹⁾ | - | x ⁽²⁾ |).

Тоді для x ⁽¹⁾ = 3, x ⁽²⁾ = 1, x ⁽³⁾ = -2 буде виконуватись:

h (x ⁽¹⁾, x ⁽²⁾ ) = 6 > 0, h (x ⁽²⁾, x ⁽³⁾ ) = 2 > 0,

h (x ⁽³⁾, x ⁽¹⁾ ) = 6 > 0,

що відповідає порушенню умови транзитивності для цих розв’язків.

Задача пошуку х^* (якщо такий елемент існує) може бути сформульована за допомогою індикатора переваг наступним чином.

Треба знайти таке х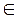^* Х, що для будь-якого х 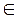Х буде виконуватись h (х^*, x) ≥ 0. Остання нерівність еквівалентна виконанню умови

.

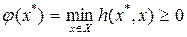Знайти таке х^* можна, максимізувавши функцію φ(х^*) на множині Х. Якщо - найкраще меню споживання існує. Якщо ж , тоді для будь-якого меню споживання існуватиме інше допустиме меню, яке переважає його. Проте й у цьому випадку як споживчий вибір можна розглядати таке х^*, яке буде максимізувати φ(х^*) або ж деякі інші функції, наприклад

,

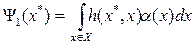або

.

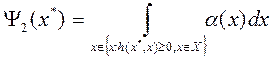Тут α(х) – деяка вагова функція, така, що .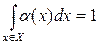

При цьому виникатиме деяка невизначеність, пов’язана з вибором, оскільки за різних функцій α(х) та за різних критеріїв як найкращі будуть обрані різні меню споживання. Проте для кожного правила вибору можна довести виконання властивостей х^*, подібних до тих, які були одержані при кардинальному вимірюванні корисності (тільки гранична корисність для кожного з цих правил буде визначатися окремо).

Дата добавления: 2014-01-07