Тема 3. Моделювання поведінки виробника

1. Моделі виробника.

2. Виробничі функції.

Розглянемо тепер модель поведінки виробника. Нехай деяке підприємство виготовляє n видів продукції, використовуючи при цьому m видів ресурсів. У моделі припускається, що підприємство має і -го ресурса у кількості b_i, , на виготовлення одиниці j -ї продукції, 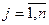, витрачається a_ij одиниць такого ресурсу. Іншими припущеннями є:

- відомий попит 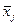на продукцію j -го виду;

- виготовлена продукція виду j (у кількості, меншої за попит) реалізується з питомим прибутком ;

- метою виробника є одержання максимального прибутку.

Тоді модель поведінки виробника є задачею лінійного програмування:

(3.1)

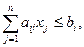
, (3.2)

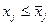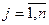, , (3.3)

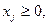
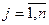. (3.4)

Тут x_j – кількість продукції виду j, що виготовляється підприємством. Множина, утворена нерівностями (3.2)-(3.4) ще зветься виробничо-технологічною множиною підприємства.

Крім (3.1)-(3.4), розглядаються також інші модифікації цієї моделі. Наприклад, якщо припустити, що підприємство може продавати (за ціною 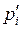) та купувати (за ціною 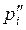) деякі з ресурсів (нехай ці ресурси утворять множину ), тоді модель набуде вигляду

,

,

, ,

, , , , .

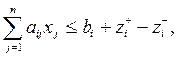
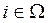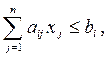
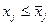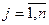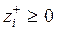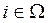Внаслідок розрахунків, проведених за моделями поведінки виробника при фіксованих цінах та обсягах ресурсів b_i можуть бути побудовані функції пропозиції та виробничі функції. Останні також розглядаються як окремий інструмент моделювання.

Виробничі функції - це залежності між обсягом виробництва та кількістю ресурсів, які витрачаються для цього. Такі залежності можуть бути одержані з моделей поведінки виробника або ж побудовані емпіричним шляхом (аналізуючи статистичні дані). Як правило, ці функції розрізняють за урахуванням взаємозаміни або взаємодоповнення чинників. Розглядаються наступні класи виробничих функцій:

1) з повною взаємозамінністю чинників, приклад – лінійна функція виробництва від кількості спожитих енергоресурсів. Нехай виробляється електроенергія за різними технологіями; припускаємо, що кожна з цих технологій витрачає енергоресурси одного виду, 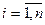- номер технології та, відповідно, ресурсу , - кількість ресурсу виду і, який витрачається на виробництво одиниці електроенергії за технологією і, b – питома енергомісткість виробництва. Якщо не враховувати інші чинники, обсяг виробництва X = bE, де Е – кількість спожитої електроенергії, z_i – обсяги споживання енергоресурсу і -го виду

,

Звідси .

Особливості такої функції – будь-яка технологія може бути повністю замінена іншою із збереженням обсягів виробництва Х і відповідний енергоресурс при цьому не витрачається.

2) з частковою взаємозамінністю чинників, приклад – Коба-Дугласа

,

якщо К = 0, Х = 0 за будь-яких L, але за додатних K, L можлива заміна, при цьому

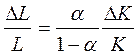
(чим більше α, тим більшою кількістю праці можна замінити ту ж саму кількість основного капіталу, тим більш технічно досконалою є економіка).

3) З повною незамінністю чинників:

приклад – функція Леонтьєва:

,

на складальному виробництві використовуються деталі n видів, α_і – кількість деталей і -го виду, що входять до складу готового виробу, z_i – кількість таких деталей, що є у підприємства, Х – кількість складених готових виробів.

Дата добавления: 2014-01-07