Дельта функция

Дельта функция () введена в математику известным физиком Дираком и поэтому часто называется функцией Дирака. Дельта функция не является функцией в обычном смысле слова, а относится к так называемым обобщенным функциям.

Существуют разные способы введения d - функции.

d - функцией будем называть функцию, удовлетворяющую следующему интегральному уравнению: 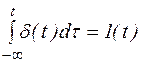(2)

Проанализируем уравнение (2).

Из (2) следует, что при t<0 (3)

Поскольку соотношение (3) справедливо для любого t<0, то это очевидно возможно лишь при условии d(t)=0 при t<0.

Пусть t>0. Обозначим через e малое положительное число. Запишем равенство:

(4)

Из (4) следует равенство:

(5)

Так как равенство (5) справедливо для любого t>e, то это возможно только при условии d(t)=0 при t>e. e - cколь угодно малое положительное число, поэтому справедливо равенство: d(t)=0 при t>0.

Для определения значения функции в момент времени t=0 в соответствии с (2) запишем

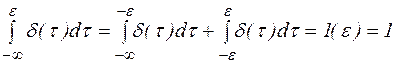, где e - малое положительное число.

В соответствии с (2) .

(6)

Равенство (6) справедливо для любого сколь угодно малого положительного e. Таким образом, площадь под кривой на бесконечно малом интервале интегрирования равняется положительному числу 1. Это возможно только при условии . Следовательно

(7)

К равенству (7) необходимо добавить соотношение 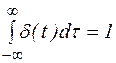(8),

которое непосредственно следует из равенства (2).

d - функцию обычно задают с помощью соотношений (7) и (8). Продифференцируем формально по t равенство (2).

На этом основании d(t) рассматривают как производную единичной ступенчатой функции.

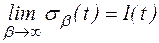Соотношение между 1(t) и d(t) пояснить с помощью следующих предельных переходов. Рассмотрим функцию . Покажем, что . Действительно

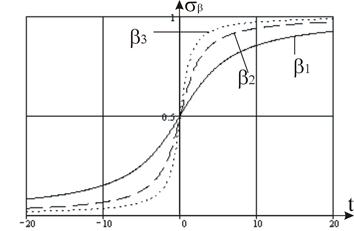рис. 3 ()

Найдем производную .

Покажем, что . Действительно

.

, ч. т. д.

На основании 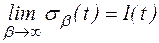, 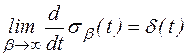. Заключаем

.

Рис. 4()

Запаздывающая d - функция определяется соотношением

Рассмотрим интеграл , полагая, что f(t) непрерывна в точке 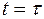. Принимая во внимание вид d(t), имеем

(9)

.

Свойство, выраженное равенством называют фильтрующим свойством d(t).

Введение d - функции позволяет дифференцировать разрывные функции. Рассмотрим функцию , которая имеет в точке разрыв первого рода.

при

Дата добавления: 2014-01-07