Коэффициент корреляции и интервал корреляции

Корреляционные функции и взаимные корреляционные функции характеризуют не только степень связи между случайными процессами, но и зависят от их дисперсии. Действительно, если, например один из процессов или 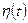весьма мало отклоняется от своего математического ожидания, то корреляционная функция будет мала, независимо от степени связи между функциями.

Для количественной характеристики степени линейной зависимости стационарных и стационарно связанных центрированных случайных процессов введём нормированные корреляционные и взаимные корреляционные функции. Они определяются соответственно выражениями

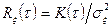, (3.10)

.

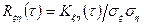Нормированные корреляционные функци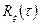и и называются коэффициентами корреляции и взаимной корреляции.

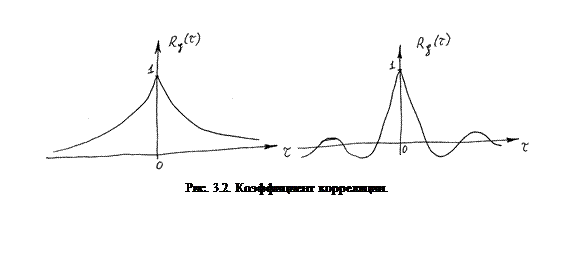Из выражения (3.10) следует (рис. 3.2)

; ; ; .

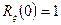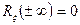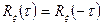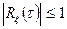Степень коррелированности случайного процесса можно характеризовать интервалом корреляции. Для стационарного в широком смысле случайного процесса всегда можно указать такой граничный интервал , при превышении которого, случайные величины и 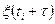для любого можно считать практически некоррелированными. В этом случае при всех 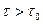абсолютное значение коэффициента корреляции остается меньше заданного значения, например 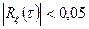. Величину называют интервалом корреляции.

Интервал корреляции определяют следующим образом

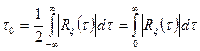. (3.11)

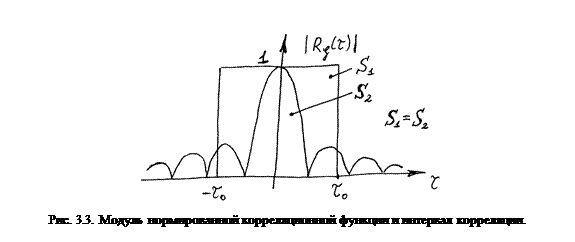
Геометрически интервал корреляции равен половине основания прямоугольника с высотой 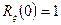, площадь которого равна площади, заключенной между криво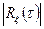й при 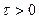и осью абсцисс (рис. 3.3).

Дата добавления: 2014-01-06