Энергетические характеристики процесса на выходе нелинейной системы

Лекция 9.

Среди нелинейных преобразований случайных процессов простейшим является такое преобразование (рис. 4.10), при котором значение выходного процесса в любой момент времени определяется только значением входного процесса в тот же момент времени:

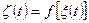, (4.33)

где – некоторая нелинейная функция.

Такое нелинейное преобразование называют безынерционным или функциональным.

К безынерционному сводятся также нелинейные преобразования, при которых входной и выходной процессы подвергаются дополнительной трансформации линейными системами (рис. 4.11), не оказывающими реакции на нелинейный элемент. Такое преобразование можно записать в форме

,

где 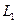и – линейные операторы, описывающие поведение линейных систем.

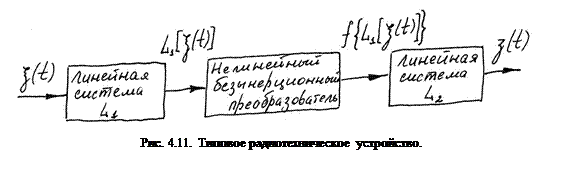
Поскольку правила преобразования характеристик случайных процессов линейными системами известны, то для изучения нелинейных преобразований достаточно рассмотреть преобразование (4.33).

В рассмотренных выше линейных системах корреляционная функция и спектральная плотность мощности выходного процесса однозначно определялись характеристикой системы и корреляционной функцией (или спектром) процесса на ее входе. Однако для определения энергетических характеристик на выходе нелинейной системы необходимо знать, по крайней мере, двумерное распределение входного случайного процесса.

Найдем энергетические характеристики случайного процесса на выходе нелинейной системы.

Пусть известны характеристика вход-выход нелинейной статистической системы

и двумерная плотность вероятности 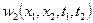случайного процесса на входе системы. Тогда, используя правила нахождения моментов функции случайных величин, для корреляционной функции случайного процесса на выходе нелинейной системы получаем

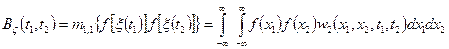. (4.34)

Если – стационарный случайный процесс, то стационарен также и процесс 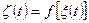на выходе нелинейной статической системы, а его корреляционная функция зависит от разности :

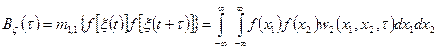. (4.35)

Если в интеграле (4.35) заменить , при 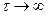, то получим выражение для среднего значения, и если заменить 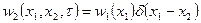, при 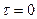, то получим выражение второго начального момента стационарного процесса на выходе:

,

.

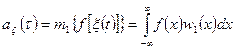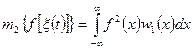Аналогично, если существует 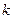-й момент процесса , то

.

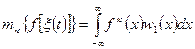Найдя корреляционную функцию стационарного случайного процесса на выходе нелинейной системы, можно, используя теорему Винера -Хинчина, т. е. совершая преобразование Фурье, получить спектральную плотность мощности этого процесса. Однако непосредственно вычислить интеграл (4.34) или (4.35), как правило, очень сложно. Поэтому целесообразно предварительно преобразовать его так, чтобы разделить переменные интегрирования в двойном интеграле.

Существует несколько методов, позволяющих найти решение интеграла (4.34).

Прямой метод вычисления корреляционной функции основан на разложении двумерной плотности вероятности в ряд по ортогональным полиномам 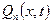, условие ортогональности которых удовлетворяет равенству

,

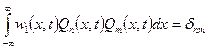где – символ Кронекера.

Второй способ вычисления интеграла (4.34) заключается в использовании представления характеристики нелинейной системы контурным интегралом. Такой подход позволяет выразить корреляционную функцию и математическое ожидание процесса на выходе системы через характеристическую функцию процесса на входе системы.

Третьи метод – метод производных позволяет получить дифференциальные уравнения, связывающие средние значения и корреляционные функции процессов на входе и выходе системы.

При выборе между первым и вторым методом ориентируются на вероятностные характеристики нелинейной системы.

Метод производных часто позволяет получить выражение корреляционной функции процесса на выходе нелинейной системы в замкнутой форме, а не в вид бесконечного ряда. Однако с помощью представления в виде ряда можно гораздо проще выполнить преобразование Фурье корреляционной функции, необходимое для определения спектральной плотности мощности.

Отметим, что эти методы пригодны также для вычисления взаимной корреляционной функции процессов и на выходе двух нелинейных систем, если известны совместная двумерная плотность вероятности процессов на входах этих систем и их характеристики. Выражение для указанной взаимной корреляционной функции имеет вид

. (4.36)

Формула (4.34) является частным случаем (4.36), когда и . Если , то (4.36) дает выражение взаимной корреляционной функции процессов на входе и на выходе нелинейной системы (при ).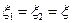

Дата добавления: 2014-01-06