Формула полной вероятности и формула обратной вероятности

Лекция 12.

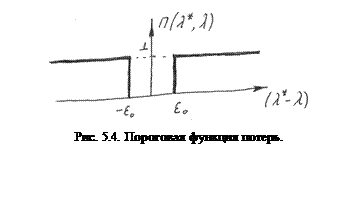
Пороговая функция потерь

Линейная функция потерь

.

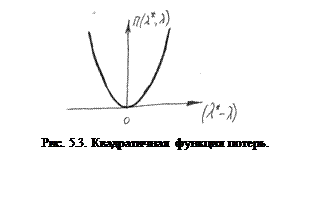Квадратичная функция потерь

. (5.3)

,

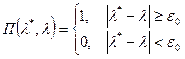где – порог для ошибки (допустимая ошибка).

Могут быть комбинированные функции потерь.

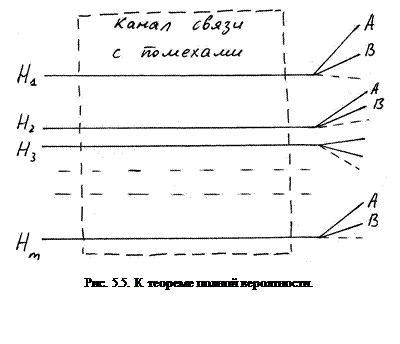
Во многих реальных ситуациях то или иное событие 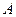может появиться лишь как случайное следствие одного из несовместимых событий , которые входят в некоторую полную группу событий и называются гипотезами. При этом термин «случайное следствие» означает, что каждая из гипотез может повлечь за собой не только исход 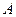, но и какие-то другие исходы. Схематически такая ситуация изображена на рис. 5.5.

Предполагается, что вероятности гипотез 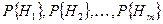и условные вероятности появления события 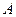при каждой из гипотез, т. е. вероятности , известны. Ставится задача, определить безусловную вероятность события 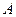, т. е. вероятность 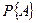, соответствующую всем возможным случаям появления события .

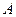Отметим, что событие 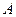появляется тогда и только тогда, когда одновременно осуществляются пары событий (см. рис. 5.5), причем эти пары событий несовместимы так же, как и сами гипотезы . Поэтому согласно теореме сложения можем написать

. (5.4)

Для определения вероятности событий можно применить теорему умножения:

.

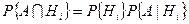В результате вместо (5.4) получим

.

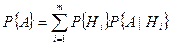Полученная формула носит название формулы полной вероятности.

Ситуация, приводящая к формуле обратной вероятности, может быть описана следующим образом. Пусть интересующее нас событие 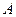может появиться лишь как случайное следствие одной из несовместимых гипотез составляющих полную группу событий (рис. 5.5). Вероятности гипотез 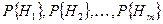и условные вероятности события 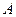при этих гипотезах 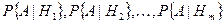известны. Пусть произведено испытание, и результатом его явилось событие 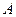. Спрашивается, с какой из гипотез следует связывать появление события ?

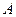Отметим прежде всего, что поскольку изложенная ситуация является вероятностной, то ответ на поставленный вопрос не может быть дан в детерминированной форме и тоже будет иметь вероятностный характер. Для решения необходимо вычислить условную вероятность каждой гипотезы при условии, что произошло событие 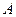, и той из гипотез, которая будет иметь наибольшую вероятность , следует отдать предпочтение.

Объясним порядок вычисления вероятностей , , 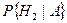…, . На основании теоремы умножения вероятностей можно для вероятности совместного появления события 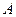и гипотезы написать

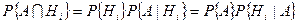. (5.5)

Отбрасывая левую часть выражения (5.5) можно записать

.

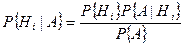При этом по формуле полной вероятности имеем

.

Следовательно,

. (5.6)

Формула (5.6) называется формулой обратной вероятности или формулой Байеса. Она имеет основополагающее значение для многих задач радиолокации, радионавигации и связи.

Рассмотрим, например, простейший канал связи с помехами, по которому могут передаваться сигналы только двух видов, условно обозначаемые далее как 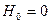и .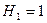

Относительную частоту следования символов 0 и 1 на передающем конце обозначим, как и ; эти вероятности можно найти путем изучения статистики сообщений. Пусть известно, что на входе канала связи на каждый 0 в среднем приходится три единицы, т. е. 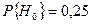и .

Особенность работы линии связи в условиях помех состоит в том, что из-за влияния помех сигналы в канале связи искажаются и могут переходить один в другой. Обозначим событие приема 0 на выходе канала связи через и событие приема 1 – через 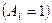, рис. 5.6.

Пусть известно, что вероятности приема 0 при передаче 0 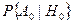и перехода 0 в 1 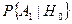равны, т. е. и . При этом в 90% всех случаев при посылке 1 она переходит в 0 и только в 10% – передается без искажений, т. е. 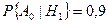и .

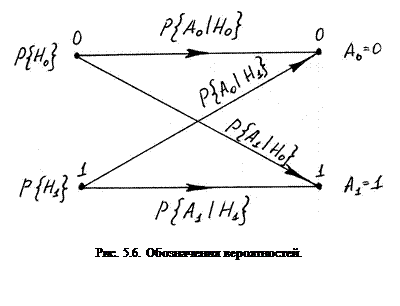Ставится вопрос, какое из значений сигнала было на входе канала связи, если на выходе была получена 1?

По формуле (5.6) найдем

,

.

Примечательно то, что вероятность появления 1 в сообщении первоначально равная 0,75, после опыта (получено получено значение 1) приобрела иное значение, в данном случае существенно уменьшилась до значения 0,375. Поэтому в подобных случаях часто говорят о доопытной (априорной) и послеопытной (апостериорной) вероятностях события.

Таким образом, согласно формуле Байеса (5.6) при определении того, имела или не имела место гипотеза следует принять во внимание первоначальные сведения о ней, характеризуемые априорной вероятностью , и результаты опыта, т. е. что произошло именно событие 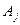(а не какое-то другое событие, которым может сопровождаться -я гипотеза ).

Дата добавления: 2014-01-06