Устойчивость линейных систем

Решения матричного уравнения

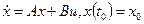(20.1)

дается формулой Коши

(20.2)

где переходная матрица представляет собой матричную экспоненту:

(20.3)

определенную как ряд:

(20.4)

В частности для свободной системы

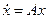и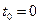

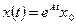
Удобный способ нахождения матричной экспоненты:

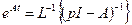(20.5)

Рассмотрим дифференциальное уравнение вида

(20.6)

Любое частное решение 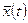вызванное начальными условиями 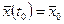может быть названо невозмущенным движением, тогда любое другое решение порожденное другими начальными условиями называется возмущенным движением. Эти решения можно изображать в виде траекторий в фазовом пространстве или в расширенном фазовом пространстве.

Пусть, например: 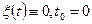и пусть невозмущенным считается движение порожденное начальным условием 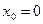, т.е. тривиальное решение . Тогда траектории могут иметь следующий вид:

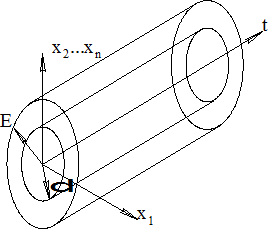
Определение 20.1. Невозмущенное движение 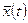системы (20.6) называется устойчивым по Лапласу, если для любого найдется , такое что из следует для всех . В противном случае оно называется неустойчивым. Неустойчивому движению соответствует траектория уходящая в бесконечность.

Определение 20.2. Невозмущенное движение 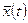называется асимптотически устойчивым если:

1. оно устойчиво по Ляпунову
2. при .

Устойчивость состояния равновесия является частным случаем рассмотренной выше устойчивости при постоянно действующем возмущении при .

Определение 20.3. Состоянием равновесия называется такое состояние, в котором система, не будучи подвержена внешним возмущениям, может оставаться сколь угодно.

Определение 20.3.а. Вектор 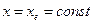называется состоянием равновесия системы 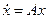(20.7)

(свободной системы), если (20.8)

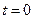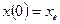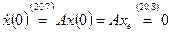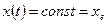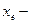Пояснение: пусть при и , тогда . Следовательно, для всех . Следовательно, состояние равновесия.

Если определитель матрицы 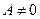, то система (20.7) имеет единственное состояние равновесия (следует из (20.8) при умножении обеих частей на ).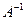

Если , то система имеет бесконечное множество состояний равновесия.

Среди собственных значений матрица 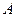имеет, по крайней мере, одно нулевое значение. Можно сказать, что состоянию равновесия 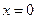соответствует невозмущенное движение при начальном условии .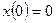

Теорема 20.1. Для устойчивости (асимптотической устойчивости) всех решений уравнения (20.6) необходимо и достаточно, чтобы было устойчиво (асимптотически устойчиво) какое-нибудь тривиальное решение (например 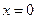) уравнения (20.7). Таким образом, свойство устойчивости зависит только от матрицы 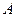. Поэтому только для линейных систем принято говорить не только об устойчивости каких-либо движений и устойчивости состояния равновесия, но и об устойчивости самой системы.

Пусть система описывается уравнением (20.7) и имеет характеристический полином 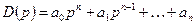(20.9)

Теорема 20.2. (основная теорема об асимптотической устойчивости). Для асимптотической устойчивости системы необходимо и достаточно, чтобы все собственные значения матрицы 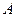и корни характеристического полинома лежали строго слева от мнимой оси.

, для всех (20.10)

Замечание: матрица 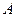и полином удовлетворяющие (20.10) называются Гурвицевыми или устойчивыми.

Доказательство: (для случая простых собственных значений).

Достаточность: пусть выполняется (20.10), рассмотрим разные случаи:

1. . С помощью преобразования приведем уравнение (20.7) к виду (20.11) где диагональная матрица 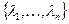. Отсюда 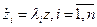(20.12) Для этого случая имеем:

при

1. 

Тогда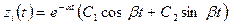

при (поскольку огибающая стремится к нулю).

Итак, 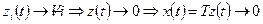при система асимптотически устойчива.

Необходимость: пусть система асимптотически устойчива. Допустим, что среди имеется, по крайней мере, хотя бы одно :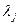

·

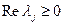
при

· ;

·

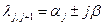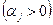
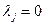
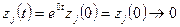(так как )

· ;

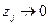
Таким образом, при , что противоречит допущению об асимптотическом движении. А это доказывает необходимость.

Если система не является асимптотически устойчивой, то она находится на границе устойчивости, что соответствует понятию устойчивости по Ляпунову.

Теорема 20.3. (без доказательства). Нулевое решение 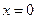уравнения 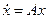(20.13)

устойчиво по Ляпунову если:

· все собственные значения матрицы 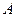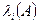имеют неположительные вещественные части.

· собственные значения с нулевой вещественной частью, являются простыми корнями минимального многочлена 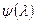матрицы 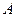. И неустойчива, если хотя бы одно из условий не выполняется.

Пример 20.1. Рассмотрим две системы второго порядка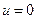

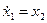
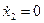
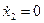
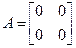
Характеристический полином:

Присоединенная матрица:

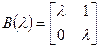
Наибольший общий делитель:

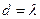
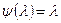
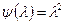
простой корень .

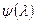двукратный корень .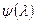

Система устойчива по Ляпунову Система неустойчива по Ляпунову

Следствие 1. Достаточное условие неустойчивости. Если среди имеется хотя бы одна с положительной вещественной частью, то система неустойчива.

Следствие 2. Если среди одно нулевое, а остальные – левые, то система устойчива по Ляпунову, причём говорят, что она находится на границе устойчивости апериодического типа. Это означает, что по окончанию переходного процесса хотя бы одна из переменных системы принимает постоянное значение, вообще говоря, отличное от нуля.

Следствие 3. Если среди имеется пара чисто мнимых, а остальные – левые, то система устойчива по Ляпунову, причём говорят, что она находится на границе устойчивости, это означает, что хотя бы одна переменная совершает незатухающие гармонические колебания.

Дата добавления: 2014-01-07