Критерий Найквиста для АФХ

Позволяет судить об устойчивости замкнутой системы по частотным характеристикам разомкнутой системы.

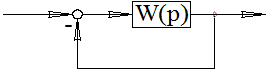
передаточная функция разомкнутой системы:

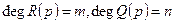
при т.е. АФХ разомкнутой системы стремится к началу координат.

Передаточная функция замкнутой системы:

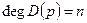
Рассмотрим вспомогательную функцию

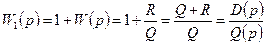
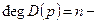характеристический полином замкнутой системы

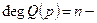характеристический полином разомкнутой системы

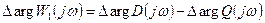(22.2)

Пример:

Первый случай:

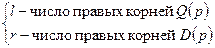
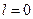(разомкнутая система асимптотически устойчива);

(по предположению)

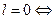лемма

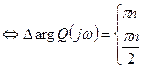
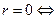лемма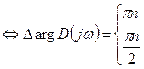

(требуется)

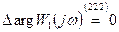
Это означает, что годограф вектора 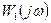при увеличении 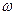не охватывает начало координат, а значит, годограф 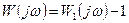не охватывает точку .

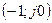Теорема 22.1. Если передаточная функция разомкнутой системы имеет только левые корни, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы при изменении не охватывала точку 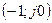или, что тоже самое (альтернативная формулировка Ципкина), разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФХ разомкнутой системы через луч равнялась нулю: .

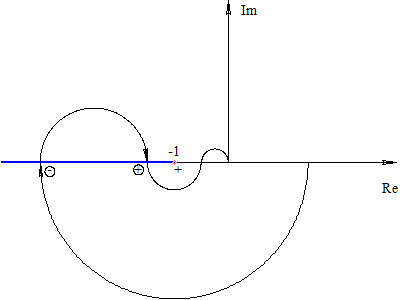
не охватывает

Пусть Гурвицев полином (корни только левые).

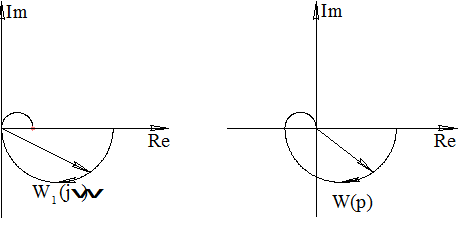
Рассмотрим возможный вид АФХ при разных .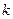

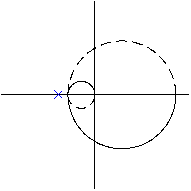АФХ разомкнутой системы не охватывает 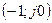или: 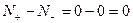следовательно, замкнутая система устойчива.

Замкнутая система находится на границе устойчивого колебательного типа.

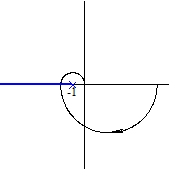АФХ разомкнутой системы охватывает 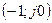или: 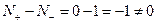следовательно, замкнутая система неустойчива.

Пусть 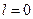, а АФХ разомкнутой системы имеет вид:

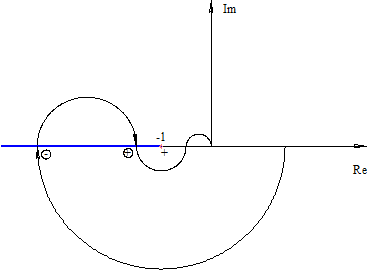
Легко увидеть, что замкнутая система асимптотически устойчива, но теряет устойчивость, как при увеличении, так и при уменьшении контурного коэффициента 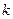. Такая система называется условно-устойчивой.

Замечание: формулировка теоремы 22.1. сохраняет свою силу, если передаточная функция разомкнутой системы кроме левых имеет также один нулевой полюс (смотри дальше).

Второй случай:

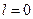, но имеется один или несколько нулевых полюсов передаточной функции разомкнутой системы.

Этот случай принципиально не отличается от первого, но имеет особенности изображения частотных функций.

Пусть

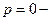полюс кратности .

Пусть 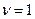, тогда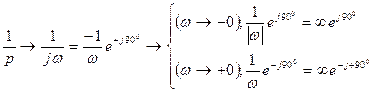

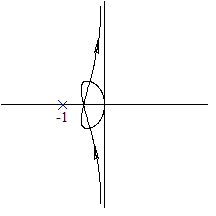
АФХ разомкнутой системы не охватывает точку 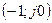следовательно, замкнутая система асимптотически устойчива. Полагаем, что нулевой полюс принадлежит левой полуплоскости, тогда при 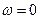скачек аргумента 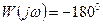(поворот вектора по часовой стрелке – дуга бесконечного радиуса).

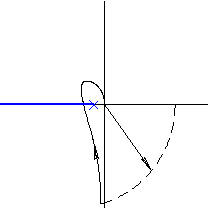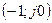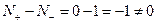АФХ разомкнутой системы охватывает точку или: следовательно, замкнутая система неустойчива. При изображении АФХ только для 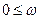дополнение при 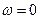всегда начинается на оси вещественных.

Пусть 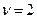, тогда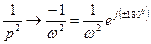

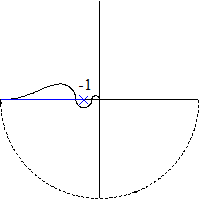
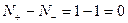следовательно, замкнутая система асимптотически устойчива.

При 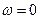полное приращение угла равно 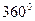. В то время как при 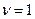дополнения не играют существенной роли (и его можно не делать, если остальные полюсы левые), поскольку не влияет на охват точк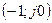и . При 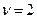дополнение существенно и является обязательным. При дополнении АФХ, приращение аргумента ЧПФ при 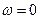составляет (если не рассматривать отрицательных частот).

Теорема 22.2. Если передаточная функция разомкнутой системы кроме левых полюсов имеет один или несколько нулевых, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы дополненное при 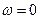дугой окружности бесконечного радиуса в направлении часовой стрелки не охватывала точку 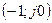, т.е. чтобы .

Третий случай:

имеется 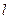правых полюсов, а остальные левые.

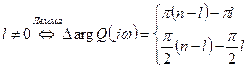
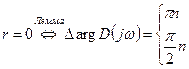, следовательно, , т.е. вектор 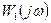должен поворачиваться вокруг начала координат (а вектор 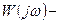вокруг точки 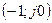против часовой стрелки 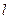раз для и 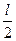раз для ).

Теорема 22.3. Если передаточная функция разомкнутой системы имеет 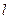правых полюсов, а остальные левые, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы охватывала точку 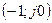в направлении против часовой стрелки 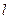раз при и раз при , или что тоже самое

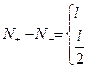
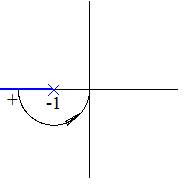
Замечание: если при 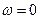АФХ начинается на луче , то это соответствует 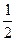перехода через этот луч, т.е. .

Теорема 22.4. Если передаточная функция разомкнутой системы имеет 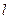правых полюсов, а остальные левые или нулевые, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы дополненное, в случае наличия нулевых полюсов при 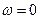, дугой бесконечного радиуса в направлении часовой стрелки охватывала точку 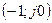. В случае наличия левых полюсов при изменении 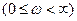, дугой бесконечного радиуса в направлении против часовой стрелки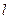 раз.

Замечание: В первом случае подпадает под эту формулировку .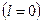

Дата добавления: 2014-01-07