Критерий Найквиста для ЛЧХ

Теорема 22.5. Если передаточная функция разомкнутой системы имеет 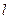правых, а остальные левые полюсов, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы в диапазоне частот, где ЛАХ разомкнутой системы лежит выше оси, разность между положительными (снизу вверх) и отрицательными (сверху вниз) переходов ЛФХ через горизонтальную прямую равнялась . Причём в случае наличия нулевых полюсов ЛФХ при 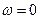должна быть дополнена надлежащим образом.

Замечание 1: дополнение при 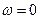должно быть выполнено так, чтобы скачёк ЛФХ составил .

Замечание 2: если 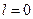, а 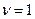, то дополнение не обязат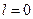ельно. Если , дополнение обязательно. Если 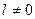дополнение обязательно независимо от .

Замечание 3: если при 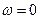ЛФХ начинается на линии с ординатой , то это соответствует 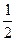перехода через эту линию.

Замечание 4: следующий случай непосредственно не подпадает под формулировку теоремы 22.5, но может быть рассмотрен исходя из основной теоремы 22.4. если во всем диапазоне частот ЛАХ разомкнутой системы лежит ниже оси абсцисс, то при 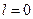замкнутая система заведомо устойчива, а при 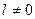неустойчива, поскольку из 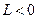следует , т.е. АФХ разомкнутой системы не может охватить точку .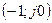

Доказательство теоремы 22.5 следует из двух фактов:

1.

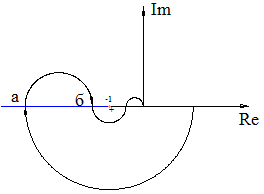Для точек перехода АФХ через луч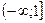 , а аргумент 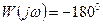(смотри точки а и б) им соответствуют точки а и б на ЛЧХ, где , а .

2.

Переходу АФХ сверху вниз соответствует переход ЛФХ через снизу вверх (точка б), и наоборот (точка а).

Следствие: (упрощенная формулировка для случая устойчивости разомкнутой системы с монотонной ЛАХ). Если в передаточной функции разомкнутой системы есть только левые полюсы и возможно еще один нулевой, а ЛАХ разомкнутой системы монотонна, то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы на частоте среза ЛФХ разомкнутой системы проходила выше уровня .

Дата добавления: 2014-01-07