
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Асиеттері
|
|
|
|
Em және Hm векторлары Гельмгольц теңдеулеріне қанағаттанады делік.
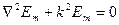 ,
,  (3)
(3)
мұнда 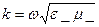 , теңдеуді шешіп Em табамыз:
, теңдеуді шешіп Em табамыз:
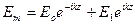 (4)
(4)
E1 – небір тұрақты вектор немесе комплекс тұрақтысы. (4) формуланы зерттеп көрейік k- параметрінің нақты және жалған қосындыларын бөліп көрейік. Ортадағы электр жоғалтуы текқана σ өткізгіштікке байланысты деп санайық 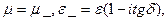 мұнда
мұнда 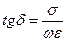 - электр жоғалтудың коэффициенті. Комплекс толқындық санын екіге бөлейік нақты және жалған санына k_=Rek_+iImk_,
- электр жоғалтудың коэффициенті. Комплекс толқындық санын екіге бөлейік нақты және жалған санына k_=Rek_+iImk_,
Rek_+iImk_=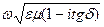 (5)
(5)
Соңғы теңдеудің екі жағын квадраттайық та нақты және жалған бөліктерін жұптайықта екі алгебралық теңдеуіне келеміз.
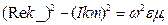 ,
, 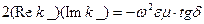 (6)
(6)
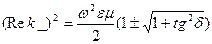 (7)
(7)
(Rek_)2 минус белгілі бола алмайды, сол спбептен + аламыз түбір алдында
Келесі белгі еңгізейік:
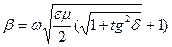 = Rek_ (8)
= Rek_ (8)
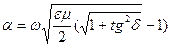 =
= 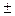 Imk_ (9)
Imk_ (9)
(6) шы теңдеуден Rek_ және Imk_ белгілері әр түрлі болуы керек
Мынандай k болуы мүмкін:
1) 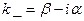 , 2)
, 2) 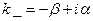 сол себептен
сол себептен 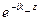 және
және 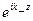 екі түрде жазыла алады 1)
екі түрде жазыла алады 1) 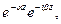 2)
2) 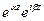
Бірінші толқынды қарастырайық 1).
Уақыттың t = to мезгілінде, z = zo нүктесінде электр кернеулігінің фазасы
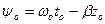 . Келесі уақытта t = to +
. Келесі уақытта t = to + 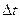 , z = zO +
, z = zO + 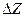 нүктесінде фаза
нүктесінде фаза

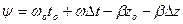 ,
, 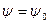 десек
десек
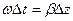 оң белгілі уақыттың өсуіне координат өсуіде оң белгілі.
оң белгілі уақыттың өсуіне координат өсуіде оң белгілі.
2) толқынды алсақ мынандай теңдеуге келеміз 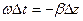 екінші толқын Z өсіне қарсы тарайды. Орта біртекті изотропты боған соң толқын текқана Z өсіне бағыттас болу керек. (4) теңдеуде бірінші қосындының фаза көрсеткіші e-ikz деп берілген, сол себептен
екінші толқын Z өсіне қарсы тарайды. Орта біртекті изотропты боған соң толқын текқана Z өсіне бағыттас болу керек. (4) теңдеуде бірінші қосындының фаза көрсеткіші e-ikz деп берілген, сол себептен  деп алған жөн.
деп алған жөн.
Ал екінші қосынды вибраторға бағытталған толқынды сипаттайлы, онда
E1 = 0. Сонымен
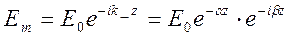 (10)
(10)
Дәл солай Hm векторына арналған Гельмгольц теңдеуінен табамыз:
 (11)
(11)
Гельмгольц теңдеуінен Em, Hm туралы басқа информация алуға болмайды. Em, Hm Максвелл теңдеулеріне қанағаттану керек. Em, Hm векторлары x және y өзгермелерге тәуелді емес, сондықтан
Ezm = 0, Hzm = 0. Сонымен Em, Hm векторлары толқын бағытына перпендикуляр болады. Бұндай толқындарды көлденең толқын деп атайды. Екінші лекцияның (13) және (14) формулаларын X және Y өстеріне проекция алсақ мынандай байланысқа келеміз:
k_Hym = 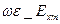 , -k_Hxm =
, -k_Hxm = 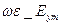 (12)
(12)
H0 = [zo, Eo ] (13)
(13)
Zc – толқындық сипаттама кедергі (Em және Hm векторларының толқын бағытына перпендикуляр құрамаларының қатынасы)
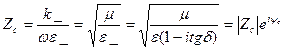 , (14)
, (14)
Мұнда
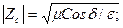
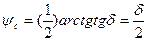 (15)
(15)
Жоғалтусыз ортада 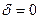 және
және 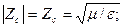
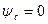 .
.
Сонымен тоқ өткізетін ортада жазықтық толқынның өрісі келесі
формуламен беріледі:
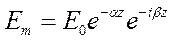 (16)
(16)
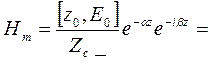
 (17)
(17)
Жоғалтусыз ортада 
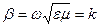 (17) формула (1) формулаға ауысыды. Меншікті өткізгіштік
(17) формула (1) формулаға ауысыды. Меншікті өткізгіштік 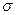 өсетін болса 0 дан
өсетін болса 0 дан 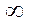 ұмтылса, ал
ұмтылса, ал
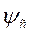 0 дан
0 дан  дейін өседі және Zc азаяды
дейін өседі және Zc азаяды 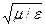 нан 0 дейін.
нан 0 дейін.
Сонымен жоғалту бар кезде сипаттама толқындық кедергі азаяды, Н магнит кернеулігі өседі берілген тұрақты Е шамасында. Бұл түсінікті әрине себебі Н тоқтың арқасында және ығысу тоғының да арқасында өседі. Жоғалту жоқ ортада текқана ығысу тоғы ғана бар. Жоғалту бар ортада сол Е шамасында және сол 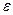 де ығысу тоғы бұрынғы шамасын сақтайды, брақта өткізу тоғы қосылады.
де ығысу тоғы бұрынғы шамасын сақтайды, брақта өткізу тоғы қосылады.
Тапқан шешімді қарастырайық. Егер Em векторы жаңғыз ғана құрамасы болса Exm , онда Hm вектордың жаңғыз ғана құрамасы болады Em ге перпендикуляр (қарастырылған мысалда Hym)
 |
E = xo E0 e-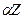 Cos(
Cos(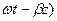
H = y0 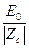 e-
e-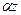 Cos
Cos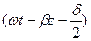 (18)
(18)
Жоғалту жоқ кезде (18) формула мынындай түрге көшеді:
E = x0 E0 Cos(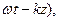 H = y0
H = y0 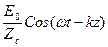 (19)
(19)
Алынған формулардан ұққанымыз біртекті изотропты ортада жазықтық толқындардың өрісі келесі қасиеттермен сипатталады:
Толқын көлденең толқын.
Е  Н (магнит өрісі электр өрісіне перпендикуляр)
Н (магнит өрісі электр өрісіне перпендикуляр)
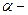 әлсіреу коэффициенті,
әлсіреу коэффициенті,
Жоғалту жоқ ортада 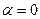 . Және Е, Н өрістері координатқа тәуелді емес.
. Және Е, Н өрістері координатқа тәуелді емес.
Егер 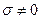 ТАЖ – тең амплитуда жазықтығы, ТФЖ- тең фазалар жазықтығы бірігеді (қабаттасады). Е және Н векторлар арасында фазалық жылжу бар. Н векторы Е векторынан фаза бойынша кешігеді
ТАЖ – тең амплитуда жазықтығы, ТФЖ- тең фазалар жазықтығы бірігеді (қабаттасады). Е және Н векторлар арасында фазалық жылжу бар. Н векторы Е векторынан фаза бойынша кешігеді 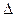
 бұрышқа. Жоғалту жоқ ортада Н векторы және Е векторы синфазды өзгереді.
бұрышқа. Жоғалту жоқ ортада Н векторы және Е векторы синфазды өзгереді.
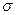 - өткізгіш коэффициенті нөлден шексізге дейін өссе,
- өткізгіш коэффициенті нөлден шексізге дейін өссе, 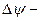 фазалық жылжу 0 ден
фазалық жылжу 0 ден  дейін өседі.
дейін өседі.

|
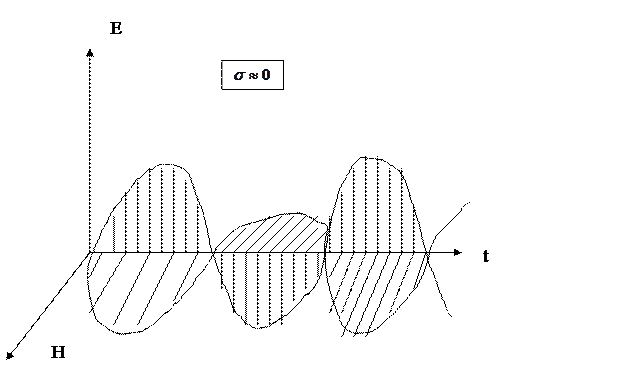
3 сурет
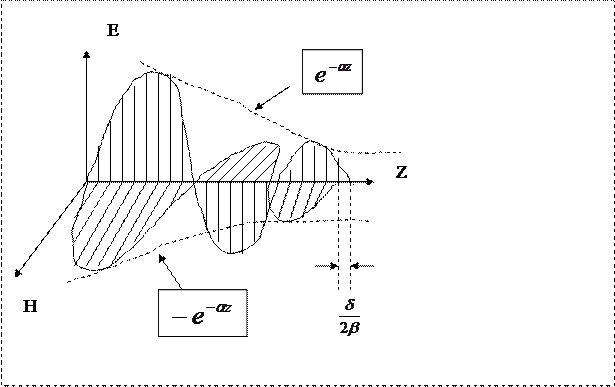
4 сурет
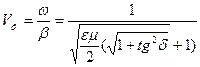 (20)
(20)
Жоғалту жоқ ортада 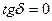 және Vф =
және Vф = 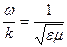
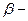 фаза коэффициенті.
фаза коэффициенті. 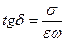
Егер орта тоқ өткізгіш блдса 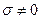 толқын ұзындығы
толқын ұзындығы
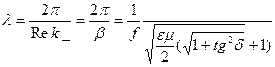 (21)
(21)
Толқын таралса сонымен бірге энергия да тасымалданады.
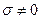 жағдайда комплексты Пойтинг векторының
жағдайда комплексты Пойтинг векторының
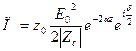 (22)
(22)
құрамында нақты және жаоған бөліктері бар. Ол дегеніміз, активты және реактивті энергия ағыны бар деген сөз.
Период шамасында орташа Пойтинг векторы Z өсімен експоненциал түрінде өзгере азаяды.
Энергия тасымалдау жылдамдығы келесі формуламен табылады:
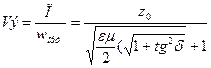 (23)
(23)
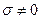 кезде энергия тасымалдау жылдамдығы жиілікке тәуелді.
кезде энергия тасымалдау жылдамдығы жиілікке тәуелді.
Толқынның қасиеттері жиілікке тәуелді болса онда бұл құбылысты дисперсия деп атайды. Ал орта диспергиялаушы орта деп аталады.
Диэлектриктегі толқындар
Диэлектрикте tg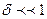 , сол себептен
, сол себептен 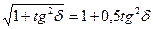 , ал
, ал
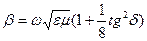 (24)
(24)
(24) теңдеуін (20) теңдеуге салсақ

 (25)
(25)
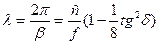 (26)
(26)
Дәл солай әлсіреу коэффициенті табылады
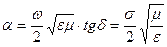 (27)
(27)
Табылған шамалар ( ) жоғалту жоқ ортадан шамалы
) жоғалту жоқ ортадан шамалы
өзгерген. Дисперсия қасиеттері шамалы көзге түседі.
Өткізгіштер ішіндегі толқындар
Өткізгіштерде (металдарда) 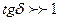 , сол себептен
, сол себептен 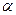 және
және 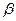 анықтайтын формулаларда бірмен санаспасақ та болады. Онда
анықтайтын формулаларда бірмен санаспасақ та болады. Онда 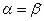 .
.
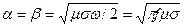 (28)
(28)
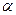 және
және 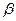 тұрақтылар жиілікпен тура пропорционал емес.
тұрақтылар жиілікпен тура пропорционал емес.
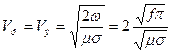 , (29)
, (29)
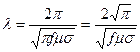 , (30)
, (30)
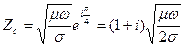 (31)
(31)
Жазықтық толқынның кейбір параметрларын диэлектрикте және металдарда салыстырайық Cu, 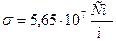 , f = 1Мгц.
, f = 1Мгц.
| вакуумде | металда |
| Vф = Vэ = 3х108 м/c | Vф = Vэ = 421 м/c |
| 
|
Zc = 120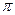 Ом Ом
| 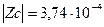 Ом Ом
|
Толқындардың өшуі
Металдағы толқынның 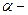 Әлсіреу коэффициенті үлкен шама, сондықтан Векторлардың амплитудасы таралу бағытында күрт құлайды, толқын тез өшеді. Z нүктесінде толқынның амплитудасы Еm(z) болсын делік, демек координатасы z +
Әлсіреу коэффициенті үлкен шама, сондықтан Векторлардың амплитудасы таралу бағытында күрт құлайды, толқын тез өшеді. Z нүктесінде толқынның амплитудасы Еm(z) болсын делік, демек координатасы z + 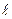 нүктесінде амплитуда Em(z +
нүктесінде амплитуда Em(z + 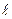 ). Қатнас, толқын
). Қатнас, толқын
 (32)
(32)
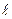 ара қашықтық өткенсоң, қанша есе амплитудасы азайғанын көрсетеді.
ара қашықтық өткенсоң, қанша есе амплитудасы азайғанын көрсетеді.
Өшу шамасын непермен (Нп) және децибелмен (дБ) өлшейді.
Децибел дегеніміз ол осы қатнастың жирма ондық логарифмы.
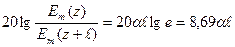 (33)
(33)
Демек 1Нп = 8,69 дБ. Сонымен 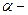 өшу коэффициенті толқынның бір метр жол өткен соң оның өшуін анықтайды. Өлшеу бірлігі Нп/м.
өшу коэффициенті толқынның бір метр жол өткен соң оның өшуін анықтайды. Өлшеу бірлігі Нп/м.
Мыспен жүретін толқынның өшуін табайық 1Мгц жийілік үшін.
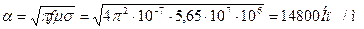
Бұл не көрсетеді? Бұл дегеніміз толқын бір миллиметр өткенде оның амплитудасы е14,8 есе азаяды ол 2,67 миллион есе. Көрсетілген мысал арқылы біздің түсінгеніміз радиотехникалық жиілікте толқын өткізгіш ішіне кірмейді практикада.
Өту тереңдігі
Егер толқын орта ішіне кіріп белгілі ара қашықтық өткенде е = 2,71 есе әлсіресе, онда бұл ара қашықтықты Өту тереңдігі деп атаймыз және оны
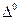 деп белгілейміз
деп белгілейміз
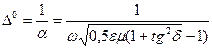 (34)
(34)
Метал үшін
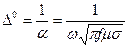 (35)
(35)
Өту тереңдігі жиілікке тәуелді. Неғұрлым f жиілік үлкен болса соғұрлым
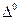 өту тереңдігі аз болады.
өту тереңдігі аз болады.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 546; Нарушение авторских прав?; Мы поможем в написании вашей работы!