
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция № 13
|
|
|
|
Лекция
Лекция
Толқындардың поляризациялануы
Z өсі бойымен таралатын жазықтық толқынның Е және Н векторларының Х және У өсіне қарасты бағытталулары толқын көзіне байланысты.
Толқын көзі қарапайым электр вибратор Z өсінде орналасқан болсын делік, ал толқын Х өсімен жоғалтусыз ортада тарғанын қарастырайық.
Жетлілікті ара қашықтықта сфералық толқын жазықтық толқынға айналады және Е өрістің бір құрамасы Ех болсын, ал Н өрісінің текқана Ну құрамасы болсын. Бұндай жазықтық толқынның жоғалтусыз ортадағы өрісі келесі теңдеумен беріледі:
E = xo E0 e-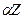 Cos(
Cos(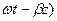
H = y0 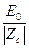 e-
e-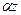 Cos
Cos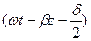 (8.18)
(8.18)
Егер бастапқы кезде t = 0 және Z = 0 нүктесінде Е векторының фазасы және Ео векторының фазалары бірдей φ = 0.
E = xo E0 Cos(
H = y0 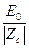 Cos
Cos (1)
(1)
Е және Н векторлары бір бірімен былай байланысқан

 (2)
(2)
Сол себептен біз текқана Е векторын қарастырамыз.
Егер Z = Const тұрақты жазықтықты алсақ, Е векторы уақыт өте өз шамасын және бағытын өзгертіп отырадыда сол жазықтықта Х өсі бойымен Е векторының ұшы түзу сызық сызып отырады, сол себептен толқын – түзу сызықты поляризацияланған толқын деп аталады. Ал
Z = Const жазықтық – поляризация жазықтығы деп аталады.
Мысалы, біз екі қарапайым электр вибраторын алсық және олардың өсін бір біріне көлденең қойсақ – бір вибраторды Z бойымен, ал екіншісін У бойымен, онда олардың I1,I2 тоқтары Z және У өстері бойымен бағытталады. Ал Z = Const жазықтақта екі өріс пайда болады Ех, Еу және Ну, Нх. Әрине бұл өрістер бір біріне қосылады Е және Н болып.
Ех + Еу = E, Ну + Нх = H (3)
Сонымен жоғалту жоқ ортада (3) формуланы толық жазуға болады:
E = xo ExmCos(ωt – kz + φ1) + y o EymCos(ωt – kz + φ2) (4)
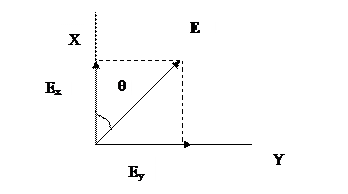
1 сурет
Егер орта тоқ жүргізетін болса 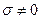 , онда (4) формулада k ны β ға ауыстыру керек және амплитуданың шамасын ескерсек:
, онда (4) формулада k ны β ға ауыстыру керек және амплитуданың шамасын ескерсек:
E = xo E0xm e-αz Cos(ωt – βz + φ1) + y o E0ym e-αz Cos(ωt – βz + φ2) (5)
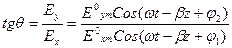 (6)
(6)
Егер 
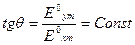 (7)
(7)
Е векторы Z өсін кесіп өтетін жазықтықта жатады, ал жазықтық болса ХОZ жазықтығымен 
Егер  мұнда
мұнда 
 (8)
(8)
Бекітілген кеңістік нүктесінде Е векторының ұшы уақыт өте түзу сызықпен қозғалады Х өсімен  бұрышын құрайды.
бұрышын құрайды.
Толқын сызықты поляризацияланған.
Енді екінші жағТолқын сызықты поляризацияланған.
Енді екінші жағдайды қарастырайық: Ех = Ey, ал фазалар айырымы
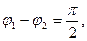
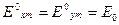 . Онда
. Онда
 (9)
(9)
 (9)
(9)
Осы теңдеулерді (6) шы формулаға қойсақ:
 осыдан
осыдан
 m – бүтін сан (10)
m – бүтін сан (10)
(10) шы теңдеуден ұққанымыз 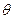 бұрышы бекітілінген z нүктесіне t уақытқа тура пропорционал. E вектор шамасы тұрақты болып тұрады.
бұрышы бекітілінген z нүктесіне t уақытқа тура пропорционал. E вектор шамасы тұрақты болып тұрады.
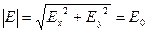 .
.
Сонымен бекітілген кеңістік нүктесінде Е векторы тұрақты бола тұра z0 бағыты бойын  жиілігімен айналады, ал Е векторының ұшы шеңбер сыза бастайды. Бұндай толқындарды – шеңбер бойымен поляризацияланған толқын деп санаймыз.
жиілігімен айналады, ал Е векторының ұшы шеңбер сыза бастайды. Бұндай толқындарды – шеңбер бойымен поляризацияланған толқын деп санаймыз.
Егер 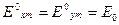 , және
, және 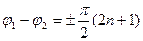 мұнда n = 0, 1, 2, 3…
мұнда n = 0, 1, 2, 3…
Сонда толқынның Е векторының ұшы шеңберді не оң жаққа қарай сызады, не сол жаққа қарай. Толқын бағытымен қарағанда Е векторының ұшы шеңберді сағат жүрісімен айналса онда біз бұл толқынды оң шеңберлі поляризацияланған деп атаймыз, егер сағат жүрісіне қарсы бұралса сол шеңберлі поляризацияланған деп атаймыз.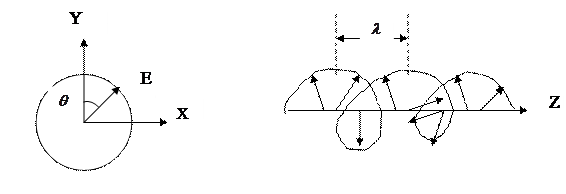
2 сурет
Е векторының комплекстік амплитудасы
 (11)
(11)
мұнда 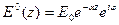 ,
,  (12)
(12)
 (13)
(13)
Егер (11) формулаға 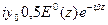 қосып және алсақ ештеме өзгермейді
қосып және алсақ ештеме өзгермейді
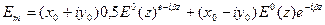 (14)
(14)
(14) формулада бірінші қосынды оң шеңберлі поляризацияланған толқын, ал екінші қосынды сол шеңберлі поляризацияланған толқын.
Егер 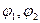 әртүрлі болса онда Е векторының ұшы эллипс сызыды, онда
әртүрлі болса онда Е векторының ұшы эллипс сызыды, онда
мұндай толқынды эллипс бойымен поляризацияланған толқын деп санаймыз.
Жоғалту бар ортада эллипстың үлкен өсі Х өсіне  бұрышқа бұралған.
бұрышқа бұралған.
 (15)
(15)

3 сурет
№ 11 Лекция
Бағытталатын толқындардың жалпы қасиеттері
1. Бағыттаушы жүйелері және бағытталатын толқындар
Кеңістіктегі еркін таралатын толқыннын басқа еріксіз толқындар болады.
Олар бағыттайтын элементтер арқылы өтеді (екі орта шекарасы, металдар, диэлектриктер, шалаөткізгіш түтіктер, стерженьдер (өзектер) т/б). Бұндай толқындарды бағытталушы толқындар деп атаймыз. Бағыттаушы жүйелер электрмагнит толқындарының энергиясын көзінен
(генератордан) тұтынушыға дейін, мысалы, таратқыштан антеннаға, қабылдау антеннасынан қабылдағыштың кірісіне ж. т/б. Cол себептен бағыттаушы жүйулерін басқаша энергия таратушы жүйесі деп те атайды.
Егер бағыттаушы жүйесінің қима ауданы не болмаса басқа параметрлары бойлық бағытта өзгермейтін болса, онда оны біз бір текті деп атаймыз. Төмендегі 1 суретте біртекті бағыттаушы жүйелері көрсетілген: а) екі сымды, б) коаксиалды, в) екі сымды экрандалған, г) симметриялық, д) бейсимметриялық, е) жолақ жүйелер, диэлектрлік толқын жетектеуші, ж) жарық жетектеуші, з) қуыс металдар толқын жетектеушілер: k) тік бұрышты, и) дөңгелек, к) эллипс тәрәзді.

1 сурет
Жүйелер ашық және жабық болады. Ашық жүйеге жауын, қар, мұз, жел, нажағай, басқа элетктрмагнит толқындар әсер етеді.
Өздерінің құрлысына байланысты толқындар көлденең, электрлік, магниттік және гибридтік түрлеріне бөлінеді.
Көлденең толқындар, немесе ТЕМ – толқындар (Т – бірінші әріп ағылшын сөзі transvers көлденең деген сөз) бұл толқынның Е және Н векторлары таралу бағытына перпендикуляр, демек бойлық құрамалары жоқ.
Электр толқындар, немесе Е- толқындар деп аталатын толқындар Е векторының құрамалары көлденең және бойлық бола алады, ал магнит өрісінің тек қана көлденең құрамасы болады сол себептен кейде ТМ – толқындар немесе көлденең магнит толқындары дейді.
Магнит толқындар, немесе Н- толқындар деп аталатын толқындар Н векторының құрамалары көлденең және бойлық бола алады, ал электр өрісінің тек қана көлденең құрамасы болады сол себептен кейде ТЕ – толқындар немесе көлденең электр толқындары дейді.
Гибрид толқындар немесе аралас толқындарда Е және Н векторларының құрамалары көлденең және бойлық бола алады.
2. Электрмагнит өрісінің көлденең және бойлық құрамаларының арасындағы байланыс
Е және Н векторларының амплитудалары біртекті ортада былай таралады:

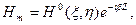 (1)
(1)
Мұнда 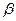 = Const (фаза коэффициенті), ал
= Const (фаза коэффициенті), ал  көлденең жазықтықта өзгеретін координаталар. Em және Hm біртекті Гельмгольц теңдеулеріне бағынады.
көлденең жазықтықта өзгеретін координаталар. Em және Hm біртекті Гельмгольц теңдеулеріне бағынады.
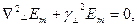
 (2)
(2)
Мұнда
 , оператор
, оператор 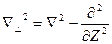 . (3)
. (3)
Ал 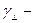 көлденең толқындық саны деп аталады.
көлденең толқындық саны деп аталады.
Егер Em және Hm векторларының бойлық құрамалары болса, онда
бағытталатын толқынның өрісін табу Ezm және Hzm құрамаларын табу
әрекетіне келтірілген, себебі көлденең құрамалары бойлық құрамалар арқылы анықталады. Максвелл теңдеулерін Х және У өстеріне проекциясын алайық, және Z – координата бойынша туынды алу
(- i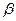 ) ға көбейтүге сәйкес екенін ескерсек
) ға көбейтүге сәйкес екенін ескерсек
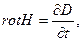
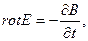 (4)
(4)

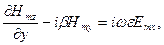
 (5)
(5)
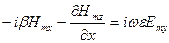 ,
, 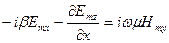
(5) ші жүйе арқылы көлденең Emx, Emy, Hmx, Hmy құрамаларын бойлық құрамалар Emz және Hmz арқылы анықтауға болады!
Түрлендіру арқылы келесі теңдеулерге келеміз:
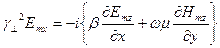 ,
,
 ,
,
(6)
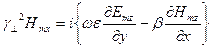 ,
,

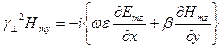 .
.
Бұл теңдеулерде көлденең Emx, Emy, Hmx, Hmy құрамаларын бойлық құрамалар Emz және Hmz арқылы байланысы көрсетілген!
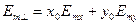 ,
,  (7)
(7)
Толық айтсақ
 ,
,  (8)
(8)
Emx, Emy шамаларын (7) теңдеуге салсақ мынандай теңдеуге келеміз:
 (9)
(9)
Векторлы түрінде (9) теңдеу:
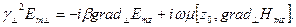 (10)
(10)
Мұнда оператор  (11)
(11)
Дәл солай магнит өрісін табуға болады
 (12)
(12)
ТЕМ толқындарында бойлық құрамалар Emz және Hmz жоқ, бірақта
(6) және (10) формулалар пайдалы болады.
Бойлық құрамалар Emz және Hmz Гельмгольц теңдеуіне бағынады.

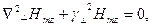 (13)
(13)
Электр, магнит және гибридтік толқындардың қасиеттері мен параметрлері
Электр, магнит және гибридтік толқындар үшін 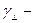 тұрақты шама нөлден ерекше. Тұрақтылығы (10) және (12) теңдеулерден (11 лекция)
тұрақты шама нөлден ерекше. Тұрақтылығы (10) және (12) теңдеулерден (11 лекция)
көрінеді. Әр тарату желісінде (13) теңдеулерді шешіп және осы жүйеге сәйкес шеткі шарттарды ескере отырып 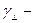 жеке табылады.
жеке табылады.
Және 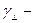 тұрақты тарату желінің формасы, өлшеміне және олардың көлденең қима ауданына және таралатын толқындар түріне байланысты.
тұрақты тарату желінің формасы, өлшеміне және олардың көлденең қима ауданына және таралатын толқындар түріне байланысты.
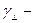 көлденең толқындық сан толқынның жиілігіне тәуелді емес.
көлденең толқындық сан толқынның жиілігіне тәуелді емес.
Фаза коэффициентін (3) формуладан табуға болады.
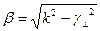 (1)
(1)
 болғандықтан түбір асты жиілікке байланысты не + не – не нөлге тең болады.
болғандықтан түбір асты жиілікке байланысты не + не – не нөлге тең болады.
екінші жағдайда 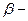 нақты сан және фазасы z координатасына тура пропорционал себебі толқын Z өсімен тұрақты фазалық жылдамдықпен таралады
нақты сан және фазасы z координатасына тура пропорционал себебі толқын Z өсімен тұрақты фазалық жылдамдықпен таралады 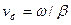 .
.
Үшінші жағдайда түбір асты  , ал
, ал 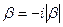 мұнда минус физикалық көзқарасынан алынған, себебі
мұнда минус физикалық көзқарасынан алынған, себебі 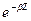 толқынның амплитудасын z координата бойымен азайтады, егер + болса амплитуда өсе береді z координата бойымен бұл мүмкін емес жағдай. Өрістің амплитудасы экспонентті азаюы энергия жоғалтуымен байланыс емес. Ал екінші жағдайда параметр
толқынның амплитудасын z координата бойымен азайтады, егер + болса амплитуда өсе береді z координата бойымен бұл мүмкін емес жағдай. Өрістің амплитудасы экспонентті азаюы энергия жоғалтуымен байланыс емес. Ал екінші жағдайда параметр  болғанда жиілік критикалык болып саналады.
болғанда жиілік критикалык болып саналады.
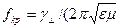 , k =
, k =  (2)
(2)
Бұл жиілікке сәйкес толқын ұзындығы
 (3)
(3)
Көлденең толқындық санды (3) теңдеуден тауып (1) теңдеуге салсақ:
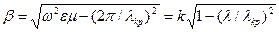 (4)
(4)
Тек қана
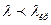 (5)
(5)
болған жағжайда 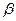 нақты сан болады.
нақты сан болады.
(5) ші теңдеуді былайда жазуға болады:
 (6)
(6)
Сонымен Е, Н және гибрид толқындар идеалды тарату желісінде таралу мүмкін егер олардың жиілігі критикалық жиілігінен үлкен болса.
(5) және (6) тең еместік толқынды тарату жілісінде толқынның таралу шарты боп саналады.
Әшейінде толқын ұзындығын анықтау амалы сияқты  деп тарату желісінде бағытталынған толқынның бір уақыт мезгілінде екі көлденең қималарының арасындағы фаза айырымы
деп тарату желісінде бағытталынған толқынның бір уақыт мезгілінде екі көлденең қималарының арасындағы фаза айырымы  ге тең болса сол араны толқын ұзындығы деп атаймыз.
ге тең болса сол араны толқын ұзындығы деп атаймыз.
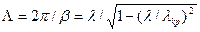 (7)
(7)
Фазалық жылдамдық
 (8)
(8)
Көріп тұрғандай 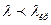 жағдайда тарату желісінде толқын ұзындығы
жағдайда тарату желісінде толқын ұзындығы  және фазалық жылдамдығы
және фазалық жылдамдығы  бір текті ортада параметрлары
бір текті ортада параметрлары  жоғалтусыз еркін таралатын толқын ұзындығынан
жоғалтусыз еркін таралатын толқын ұзындығынан 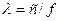 және фазалық жылдамдығынан
және фазалық жылдамдығынан 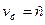 үлкен.
үлкен.
Ескерту Е, Н және гибрид толқындардың фазалық жылдамдықтары жиілікке тәуелді. Бұл құбылысты толқын дисперсиясы деп атайды.
 жағдайда фазалық жылдамдық шексіздікке тең болады, ал жиілік өскенде жарық жылдамдығына жақындайды.
жағдайда фазалық жылдамдық шексіздікке тең болады, ал жиілік өскенде жарық жылдамдығына жақындайды.

1 сурет
Е толқындар және Н толқындар үшін (3) критикалық жиілік, (4) критикалық толқын ұзындығы, (5) фаза коэффициенты және (8) фазалық жылдамдық формулардың мағаналары бірдей.
Әрине Е толқындардың  формуласындағы
формуласындағы 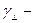 көлденең фазалық саны Н толқындар үшін
көлденең фазалық саны Н толқындар үшін 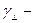 бірдей болмайды, сол сияқты басқа параметрлары
бірдей болмайды, сол сияқты басқа параметрлары  бірдей болмас.
бірдей болмас.
Енді сипаттама толқындық кедергісін қарастырған тоқындарға тауып көрейік. Анықтама бойынша сипаттама толқындық кедергісі тоқынның таралу бағытына перпендикуляр Em және Hm құрамаларының қатынасына тең.
Мысалы, Е толқындар үшін көлденең құрамалары:
 (9)
(9)
 (10)
(10)
Бұл теңдеулер 10 лекциядағы (10), (12) формулардан шығада, егер
Hmz =0 деп санасақ Е толқындар үшін.
(9) шы формуладан 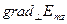 алып (10) формулаға еңгізсек мынандай
алып (10) формулаға еңгізсек мынандай
мағана табамыз:
 (11)
(11)
Cол сияқты осындай теңдік келесі векторларға орындалады

 (12)
(12)
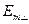 және
және  бір біріне перпендикуляр (
бір біріне перпендикуляр ( да бір біріне перпендикуляр).
да бір біріне перпендикуляр).
Е толқындар үшін  (13)
(13)
мұнда 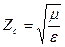
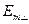 және
және  арасындағы байланыс
арасындағы байланыс
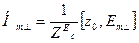 (14)
(14)
Е толқындар сипаттама кедергісі толқын ұзындығына тәуелді
Егер 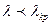 ,
, 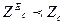
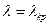 ,
, 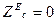 (15)
(15)
 ,
,
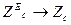
2 суретте графиктері көрсетілген
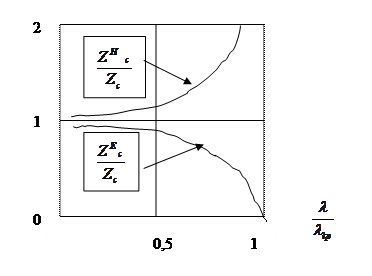
2 сурет
Аналогты түрде Н толқындар үшін сипаттама кедергісін табамыз.

 (16)
(16)
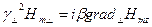 (17)
(17)
(17) ші формуладан  алып (16) формулаға салсақ:
алып (16) формулаға салсақ:
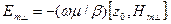 (18)
(18)
Теңдеудің екі жағын z0 ға векторлы көбейтіп екі жерде векторлы көбейтуді ашып осы теңдеуге келеміз:
 (19)
(19)
мұнда
 (20)
(20)
Н толқындар үшін 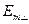 және
және  бір біріне перпендикуляр
бір біріне перпендикуляр
( да бір біріне перпендикуляр).
да бір біріне перпендикуляр).
Н толқындар сипаттама кедергісі толқын ұзындығына тәуелді
Егер 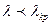 ,
, 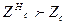
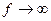 ,
, 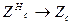 (21)
(21)
График 2 суретте көрсетілген.
Екі сымды жүйе
Бір біріне параллель екі сымдар бойымен тоқ жүреді, біреісінде ары, ал екіншісінде бері. Бұндай сымдарда жұп толқындар таралсын (екі тактылы толқындар), ал фазалары қарама қайшы (екі толқынның бағыттары керісінше).

1 Сурет
Декарт жүйесін пайдаланамыз.
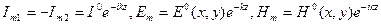 ,
,
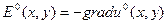 ,
, 
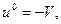 (екінші сымда)
(екінші сымда)
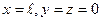 (бірінші жіп),
(бірінші жіп),  (екінші жіп).
(екінші жіп).
 - бойлық заряд тығыздығы.
- бойлық заряд тығыздығы.

 (1)
(1)
Бұнда
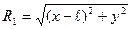 ,.
,.
Идеалды екі сымды жүйесінде тоқтар мен зарядтар бет жазықтығында болады. Комплексты тығыздықтарының амплитудалары
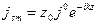 ,
, 
 бір бірімен
бір бірімен
келесі байланыста 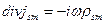 бұдан шығатыны
бұдан шығатыны
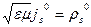 әрине келесі байланыста абзал
әрине келесі байланыста абзал 
 көшсек
көшсек 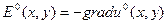 ескеріп, сонда (1) формула
ескеріп, сонда (1) формула
былай жазылады:
 (2)
(2)
Магнит өрісіне көшетін болсақ 
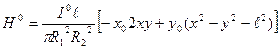 (3)
(3)
Сонымен (2) және (3) формулар арқылы ТЕМ толқындардың структурасын таптық (2 сурет).
 |

3 сурет
Магнит өрінсін біле тұра (3) формула, сыммен ағатын тоқтың тығыздығын табуға болады, мысалы, бірінші сым. Цилиндр координат жүйесін еңгізейік  декарт координат жүйесімен байланыста.
декарт координат жүйесімен байланыста.
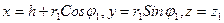 . (4)
. (4)
Бірінші сымда тоқ тығыздығы

 мұнда
мұнда
 , мұнда
, мұнда 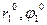 - координат орттары.
- координат орттары.
 . Есептеуін жіберіп соңғы нәтижесін жазайық:
. Есептеуін жіберіп соңғы нәтижесін жазайық:
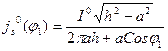 (5)
(5)

4 Сурет
Қортылған формулалардан тоқ сымның периметры бойынша біркелкі таралмаған. 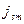 шамасы өседі
шамасы өседі  . Егер
. Егер  болса біркелкіеместік нашар байқалады сол себептен әр сымда тоқтың таралуы өске симметриялы болады. Сымдар бір – біріне жақындағанда тоқтың біркелкі еместілігі өседі. Бұл жағдай жүйеде электр жоғалтуына келтіреді.
болса біркелкіеместік нашар байқалады сол себептен әр сымда тоқтың таралуы өске симметриялы болады. Сымдар бір – біріне жақындағанда тоқтың біркелкі еместілігі өседі. Бұл жағдай жүйеде электр жоғалтуына келтіреді.
Бұл құбылысты жақындық эффекті деп атайды.
Екі сым жүйесіне және екі тактылы толқындар үшін 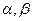 коэффициенттері Зомерфельд бірінші болып шығарған
коэффициенттері Зомерфельд бірінші болып шығарған
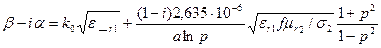 , (6)
, (6)
Мұнда 

 .
.
Лекция № 14
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1757; Нарушение авторских прав?; Мы поможем в написании вашей работы!