Свойства непрерывной функции

Свойство 1.

Если:

1) 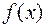непрерывна в точке 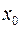относительно множества ;

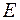2)

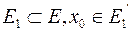
тогда 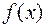является непрерывной в точке 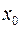относительно .

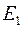Свойство 2. Для любой фиксированной окрестности точке 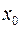(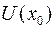) непрерывность функции 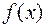в точке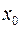относительно 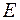равносильно непрерывности 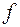в точке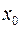относительно .

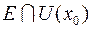Свойство 3. Если множество 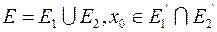, тогда непрерывность функции 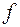в точке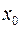относительно множества 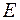равносильно непрерывности 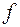как относительно 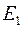, так и относительно .

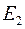Замечание: Если 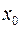в свойстве 3 является предельной только для одного из множеств(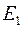или 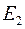), то непрерывности функции 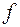относительно всего 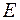будет равносильно непрерывности относительно этой части.

Свойство 4(предельный переход под знаком непрерывной функции).

Если:

1) 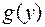непрерывна в точке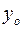относительно множества ;

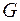2) , причем область значения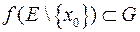

тогда предел сложной функци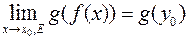иили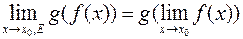

Следствие (из свойства 4):

Теорема(о непрерывности сложной функции):

Если:

1) 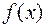непрерывна в точке 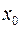относительно множества

2) 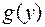непрерывна в точке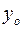относительно множества ;

тогда сложная функция 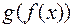будет непрерывна в точке 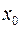относительно множества .

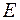Свойство 5. Если 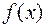непрерывна в точке 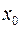относительно множества 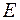, то модуль 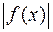также будет непрерывна в точке 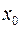относительно множества .

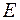Пример:

-непрерывна тоже.

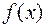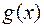Свойство 6(непрерывность результатов арифметических действий на непрерывных функциях): Если и непрерывны в точке 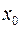относительно 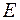, то их сумма , произведение , отношение будут непрерывны в точке 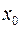относительно множества .

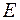Следствие. Многочлен и дробно-рациональные функции непрерывны во всех точках своей области определения..

- непрерывная функция.

1)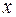- непрерывная функция

2) - непрерывная функция

3) - непрерывная функция

Определение. Функция 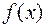называется непрерывной в точке 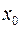относительно 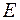справа(слева), если она непрерывна в точке 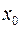относительно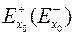

Пример:

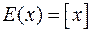
Дата добавления: 2014-01-06