Метод гілок і меж

Цей метод точного вирішення ЗЦЛП найчастіше використовується на практиці. Він полягає в наступному.

Спочатку вирішується ослаблена задача. Якщо отримане оптимальне рішення цілочислове, то ЗЦЛП вирішена. Якщо ж оптимальне рішення ЗЛП не є цілочисловим, то робимо "розгалуження" у такий спосіб. Нехай змінна х_s прийняла в оптимальному рішенні значення q_s, що не є цілим. Тоді розглядаємо дві ЗЦЛП. Перша виходить додаванням обмеження х_s <=[q_s], друга – додаванням обмеження х_s >=[q_s] + 1, де [q_s] - ціла частина числа q_s.

Кожна із цих двох задач аналогічним способом може розбитися ще на дві задачі і т.д.

Якщо в результаті вирішення якої-небудь із задач виходить цілочисловий оптимальний план, то значення А цільової функції при цьому плані відіграє роль "межі": якщо в результаті вирішення чергової ЗЛП з'ясується, що оптимальне значення цільової функції "гірше" А, тоді така задача "не гілкується".

Недолік методу гілок і меж полягає в тому, що часто оптимальне рішення ЗЦЛП досягається після дуже великої кількості розгалужень.

Повернемося до ЗЦЛП прикладу 1.

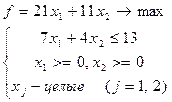
Використовуємо геометричний метод вирішення для відшукання оптимальних планів ослаблених задач.

Дата добавления: 2014-01-07