Загальна постановка й різновиди задач математичного програмування

Оптимальний план оптимальний план

Вихідна ЗЦЛП №1

(оптимальний план )

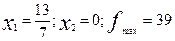оптимальний план ОПР порожня.

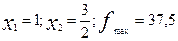
х₁=1, х₂=1, f_max=32 х₁=, х₂=2, f_max=37

A=32- межа

оптимальний план ОПР порожній

х₁=0, х₂=, f_max=35,75

Оптимальний план ОПР порожній

х₁=0, х₂=3, f_max=33>A

Оптимальний план ЗЦЛП: х₁=0, х₂=3, f_max=33.

Математичне програмування - велика галузь знань. Ми розглянули далеко не повністю один з розділів - лінійне програмування.

Загальна математична схема задачі математичного програмування така: дана деяка функція

z = f(x₁, x₂,..., x_n) (7.1)

і деяка система обмежень, накладених на змінні x₁, x₂,..., x_n:

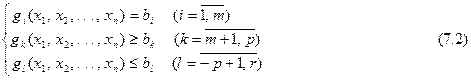
Потрібно знайти такий набір значень змінних x₁, x₂,..., x_n, що задовольняє обмеженням (7.2), і при цьому мінімізує або максимізує функцію (7.1).

Якщо всі функції, що фігурують в (7.1) і (7.2), лінійні, то ми маємо ЗЛП. У протилежному випадку виходить задача нелінійного програмування.

Для задач нелінійного програмування немає такого універсального методу вирішення, яким є симплекс-метод для ЗЛП. Тільки для вузьких класів задач нелінійного програмування розроблені точні методи, основна маса вирішується приблизно.

У деяких задачах математичного програмування ОПР складається з дискретної множини точок. Такі задачі називаються дискретними оптимізаційними задачами. Наприклад, якщо в ЗЛП зажадати, щоб змінні приймали тільки цілі значення, то вийде дискретна оптимізаційна задача - задача цілочислового лінійного програмування. Дискретні задачі, як правило, складніші безперервних. Із задач дискретної оптимізації в теперішні часи проводяться інтенсивні наукові дослідження.

Важливою галуззю є й динамічне програмування. Тут вивчаються методи поетапного вирішення оптимізаційних задач. Такі методи використовуються в особливо складних задачах. Наприклад, при складанні плану роботи заводу на рік доцільно розбити рік по місяцях і план роботи на кожний місяць погоджувати із планами на попередні й наступні місяці.

Нарешті відзначимо, що зустрічаються задачі математичного програмування, в яких вихідні дані є випадковими величинами. Такі задачі вивчає стохастичне програмування. Стохастичне програмування використовує теоретико-імовірнісні, статистичні й оптимізаційні методи.

З математичного програмування написано вже багато книг. Література, що приводиться - незначна частина їх. Але в ній можна знайти виклад основних положень математичного програмування, а також посилання на інші джерела.

ЛІТЕРАТУРА

1. Крушевский А.В., Зшивальників К.М. Математичне програмування й моделювання в економіці.-К.: Вища шк., 1979

2. Ковалів Ю.Н., Кузубов В.М., Волощенко А.Б. Математичне програмування.-М.: Высш.шк.,1980

3. Таха X. Введення в дослідження операцій. (В 2-х книгах).-
М.:Мир,1985

4. Міну М. Математичне програмування. Теорія й
алгоритми.-М.: Наука, 1990.

ЗМІСТ

1. РІШЕННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ МЕТОДОМ ГАУСА - ЖОРДАНА.......................................................................... 4

1.1. Основні поняття....................................................4

1.2. Приведення системи лінійних рівнянь до жорданової форми.... 5

1.3. Поняття загального, часного й базисного рішень............. 7

2.ЗАГАЛЬНІ ВЛАСТИВОСТІ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ

2.І. Приклад задач лінійного програмування – задача про використання обладнання.................................................... 7.

2.2. Задача про використання сировини......................... 9

2.3. Задача складання раціону (задача про дієту)..................9

2.4. Загальна постановка задач лінійного програмування (ЗЛП).....10

2.5. Геометричний метод рішення ЗЛП..........................11.

2.6. Канонічний вигляд ЗЛП...................................15

2.7. Поняття опорного плану ЗЛП.............................. 16

3. СИМПЛЕКСНИЙ МЕТОД РІШЕННЯ ЗЛП

3.1. Загальна характеристика і основні етапи симплекс – методу.....17

3.2.Табличний вид ЗЛП. Симплекс – таблиці..................... 18

3.3. Умова оптимальності опорного плану........................20

3.4. Умова нерозв'язності ЗЛП через необмеженість знизу на ОПР цільовій функції..................................................20

3.5. Перехід до нового опорного плану..........................21

3.6. Табличний симплекс-алгоритм............................. 23

3.7. Відшукання початкового опорного плану ЗЛП методом штучного базису......................................................... 28

3.8. Виродженість опорного плану. Зациклення....................34

4. ДВОЇСТІСТЬ У ЛІНІЙНОМУ ПРОГРАМУВАННІ

4.1. Економічна інтерпретація двоїстих задач.....................35

4.2. Поняття двоїстої задачі....................................36

4.3. Теореми двоїстості........................................37

5. ТРАНСПОРТНА ЗАДАЧА

5.1. Задача про перевезення.................................... 39

5.2. Загальна постановка транспортної задачі......................40

5.3. Відшукання початкового опорного плану.................... 41 5.4. Цикли перерахування......................................43

5.5. Потенціали.............................................. 46.

5.6. Алгоритм вирішення транспортної задачі методом потенціалів...49

5.7. Відкриті транспортні задачі................................ 51

6. ЦІЛОЧИСЛОВЕ ЛІНІЙНЕ ПРОГРАМУВАННЯ

6.1. Загальна постановка задачі цілочислового лінійного програмування (ЗЦЛП)..........................................................53

6.2. Цілочислова задача про використання сировини.................54

6.3. Задача про рюкзак..........................................55

6.4. Вирішення ЗЦЛП методом округлення........................ 55

6.5. Метод гілок і меж...........................................56

7. ЗАГАЛЬНА ПОСТАНОВКА І РІЗНОВИДИ ЗАДАЧ МАТЕМАТИЧНОГО ПРОГРАМУВАННЯ.............................................. 58

Література...................................................... 59

Зміст.............................................................59

Дата добавления: 2014-01-07