
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Система обмежень має три одиничних вектори - А4, А5 та А4 . Вони створюють базис
Можемо записати симплексну таблицю і знайти оптимальне рішення.
| Базис | Сi базис | План А0 | 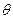
| ||||||
| А1 | А2 | А3 | А4 | А5 | А6 | ||||
| А4 | |||||||||
| А5 | |||||||||
  А6 А6
| -3 | ||||||||
| Zj - Cj | -9 | -1 | -6 | ||||||
| А4 | -2 | 108/23 | |||||||
 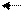 А5 А5
| -2 | 58/13 | |||||||
| А3 | -3/2 | 1/2 | 1/2 | - | |||||
| Zj - Cj | -10 | ||||||||
| А4 | 754/13 | -23/13 | 26/13 | ||||||
| А1 | 26/13 | 1/13 | -2/13 | ||||||
| А3 | 91/13 | ½ | 3/26 | 7/26 | |||||
| Zj - Cj | 572/13 | 15/13 | 19/13 |
Оскільки всі Zj - Cj 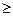 0 ми знайшли оптимальний план, який надає мінімального значення цільовій функції. Оптимальній план має вигляд:
0 ми знайшли оптимальний план, який надає мінімального значення цільовій функції. Оптимальній план має вигляд:
Yопт( y1 = 26/13,.y2 = 0,.y3 = 91/13,.y4 = 754/13,.y5 = 0.y6 = 0),
Fmax = 572/13
Знайдемо рішення вихідної задачі:
Х = Сбаз* D-1 = (0,1,6) * 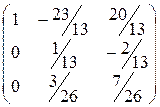 = (0, 10/13, 19/13)
= (0, 10/13, 19/13)
Zmin = 120 * 0 + 42 * 10/13 + 8 * 19/13 = 572/13
Оскільки Fmax = Zmin задача розв’язана вірно
Приклад. Деяке підприємство займається виробництвом чотирьох видів продукції А, В, С, Д, використовуючи для цього три види ресурсів І,ІІ,ІІІ. Норми витрат ресурсів на одиницю кожної продукції наведено в таблиці.
| Вид ресурсу | Норма витрат на одиницю продукції за видами | Запас ресурсу | |||
| А | В | С | Д | ||
| І | |||||
| ІІ | |||||
| ІІІ |
Відома ціна одиниці продукції кожного виду: А-2 ум. од., В-4 ум. од., С-3 ум. од., Д-4 ум. од. Визначити план виробництва продукції кожного виду в умовах обмеженості ресурсів, який дає підприємству найбільший доход.
а) записати математичні моделі прямої та двоїстої задач;
б) записати оптимальні плани прямої та двоїстої задач, виконати їх економічний аналіз;
в) визначити статус ресурсів, що використовуються для виробництва продукції, та рентабельність кожного виду продукції;
г) обчислити інтервали стійкості двоїстих оцінок стосовно зміни запасів дефіцитних ресурсів;
д) розрахувати інтервали можливих змін ціни одиниці рентабельної продукції.
Розв’язання:
а) Математичні моделі прямої та двоїстої задачі мають такий вигляд:
Пряма задача: 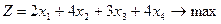 ;
;
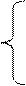
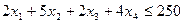 ;
;
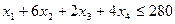 ;
;
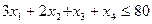 ;
;
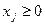
де 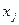 - обсяг виробництва продукції
- обсяг виробництва продукції 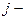 го виду.
го виду.
Запишемо симплекс – таблицю, що відповідає оптимальному плану поставленої задачі.
| Базис | 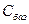
| План | |||||||
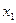
| 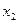
| 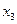
| 
| 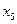
| 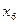
| 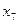
| |||
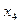
| -2 | 1/2 | 1/2 | -1 | |||||
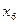
| -1 | -1 | |||||||
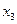
| 3/2 | -1/2 | |||||||
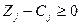
| 5/2 | 1/2 |
Двоїста задача: 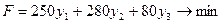
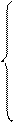
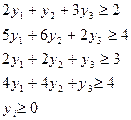
де 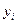 - оцінка одиниці
- оцінка одиниці 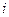 -го виду ресурсу.
-го виду ресурсу.
б) З наведеної симплекс таблиці дістаємо

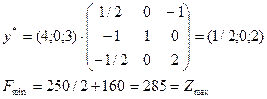
Оптимальний план прямої задачі передбачає виробництво лише двох видів продукції С і Д у кількості відповідно 35 та 45 од. Випуск продукції А та В не передбачається (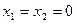 ). Додаткові змінні
). Додаткові змінні 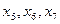 характеризують залишок (невикористану частину) ресурсів відповідно І,ІІ та ІІІ. Оскільки
характеризують залишок (невикористану частину) ресурсів відповідно І,ІІ та ІІІ. Оскільки 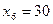 , другий ресурс використовується в процесі виробництва не повністю, а перший та третій ресурси – повністю (
, другий ресурс використовується в процесі виробництва не повністю, а перший та третій ресурси – повністю (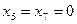 ).
).
При такому оптимальному плані виробництва продукції та використання ресурсів підприємство отримує найбільший доход у розмірі 285 ум. од.
План двоїстої задачі дає оптимальну систему оцінок ресурсів, що використовуються у виробництві. Так, 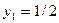 та
та 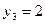 відмінні від нуля, а ресурси І та ІІІ використовуються повністю. Двоїста оцінка
відмінні від нуля, а ресурси І та ІІІ використовуються повністю. Двоїста оцінка 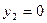 і відповідний вид ресурсу не повністю використовується при оптимальному плані виробництва продукції. Це підтверджується також попереднім аналізом додаткових змінних оптимального плану прямої задачі. Така оптимальна система оцінок дає найменшу загальну вартість усіх ресурсів, що використовуються на підприємстві
і відповідний вид ресурсу не повністю використовується при оптимальному плані виробництва продукції. Це підтверджується також попереднім аналізом додаткових змінних оптимального плану прямої задачі. Така оптимальна система оцінок дає найменшу загальну вартість усіх ресурсів, що використовуються на підприємстві 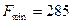 ум. од.
ум. од.
в-г) Статус ресурсів можна визначити підстановкою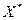 у систему обмежень прямої задачі.
у систему обмежень прямої задачі.
Якщо обмеження виконується як рівняння, то відповідний ресурс дефіцитний, у противному разі - недефіцитний.
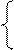
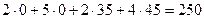 ресурс І дефіцитний
ресурс І дефіцитний
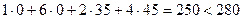 ресурс ІІ недефіцитний
ресурс ІІ недефіцитний
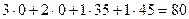 ресурс ІІІ дефіцитний
ресурс ІІІ дефіцитний
Розрахуємо інтервали можливої зміни обсягів дефіцитних ресурсів, у межах яких двоїсті оцінки 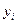 залишаються на рівні оптимальних значень.
залишаються на рівні оптимальних значень.
Приріст (зміну) запасу ресурсу І позначимо 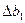 . Тоді, якщо
. Тоді, якщо 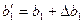 , то новий оптимальний план
, то новий оптимальний план
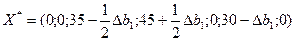 .
.
Єдина вимога, яку можна поставити до можливих нових оптимальних значень, це умова невід’ємності, тобто

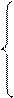
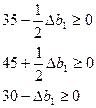
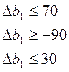

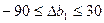
Це означає, що коли запас ресурсу І збільшиться на 30 ум. од. або зменшиться на 90 ум. од., то оптимальною двоїстою оцінкою ресурсу І залишиться 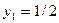 . Отже, запас ресурсу І може змінюватись у межах
. Отже, запас ресурсу І може змінюватись у межах
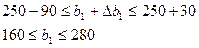
Згідно з цим максимально можливий доход підприємства перебуватиме в межах:

а оптимальний план виробництва продукції:
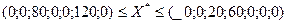
Аналогічно розраховується інтервал стійкості двоїстої оцінки 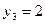 дефіцитного ресурсу ІІІ:
дефіцитного ресурсу ІІІ:

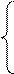

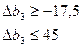
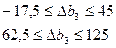
Отже, якщо запас ресурсу ІІІ збільшиться на 45 ум. од. або зменшиться на 17,5 ум. од., то двоїста оцінка 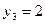 цього ресурсу залишиться оптимальною. Згідно із цим можливий доход підприємства та оптимальний план виробництва продукції перебуватиме у межах
цього ресурсу залишиться оптимальною. Згідно із цим можливий доход підприємства та оптимальний план виробництва продукції перебуватиме у межах

Слід зазначити, що визначені інтервали стосуються лише випадків, коли змінюється тільки один ресурс, а запаси всіх інших фіксовані. При одночасній зміні обсягів усіх або кількох ресурсів підхід до визначення нового оптимального плану дещо інший.
Оцінка рентабельності продукції, що виготовляється на підприємстві, виконується за допомогою двоїстих оцінок та обмежень двоїстої задачі, які характеризують кожний вид продукції.
Підставимо 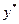 у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.
у систему обмежень двоїстої задачі. Якщо вартість ресурсів на одиницю продукції (ліва частина) перевищує ціну цієї продукції (права частина), то виробництво такої продукції для підприємства недоцільне. Якщо ж співвідношення виконується як рівняння, то продукція рентабельна.
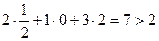 продукція А нерентабельна
продукція А нерентабельна
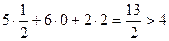 продукція В нерентабельна
продукція В нерентабельна
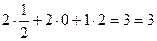 продукція С рентабельна
продукція С рентабельна
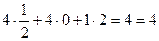 продукція Д рентабельна
продукція Д рентабельна
Аналогічні результати можна дістати, проаналізувавши додаткові двоїсті оцінки, величина яких показує, наскільки вартість ресурсів перевищує ціну одиниці відповідної продукції. Тому, якщо додаткова змінна двоїстої задачі дорівнює нулю, то продукція рентабельна. І, навпаки, якщо 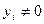 , то відповідна продукція нерентабельна.
, то відповідна продукція нерентабельна.
Додаткові змінні двоїстої задачі розміщуються в оцінковому рядку останньої симплекс-таблиці у стовпчиках 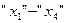 . Їх оптимальні значення
. Їх оптимальні значення 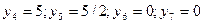 . тому продукція А і В нерентабельна, а продукція С і Д рентабельна.
. тому продукція А і В нерентабельна, а продукція С і Д рентабельна.
д) Під впливом різних обставин ціна одиниці продукції на підприємстві може змінюватися. Тому дуже важливо знати, у межах яких змін ціни продукції кожного виду оптимальний план її виробництва залишається таким 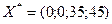
Для визначення інтервалів зміни коефіцієнтів цільової функції скористаємось тим, що при цьому оптимальна симплекс – таблиця зберігає свій вигляд за винятком елементів оцінкового рядка. Нові оцінки 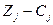 мають задовольняти умову оптимальності задачі максимізації, тобто бути невід’ємними.
мають задовольняти умову оптимальності задачі максимізації, тобто бути невід’ємними.
Величину зміни коефіцієнта 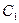 позначимо
позначимо  . Оскільки
. Оскільки 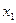 - небазисна змінна, то в симплекс – таблиці зміниться лише відповідна оцінка
- небазисна змінна, то в симплекс – таблиці зміниться лише відповідна оцінка 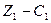 :
:
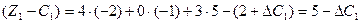
За умови 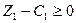 дістанемо нерівність
дістанемо нерівність  , тобто
, тобто 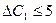 . Це означає, що коли ціна одиниці продукції А збільшиться не більш як на 5 ум. од., то оптимальним планом виробництва продукції на підприємстві все одно залишиться
. Це означає, що коли ціна одиниці продукції А збільшиться не більш як на 5 ум. од., то оптимальним планом виробництва продукції на підприємстві все одно залишиться 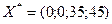 .
.
Лише максимальний доход зміниться на величину 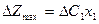
Аналогічно розраховується інтервал зміни коефіцієнта 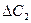 :
:
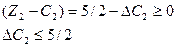
При збільшенні одиниці продукції В на 5/2 ум. од. оптимальний план виробництва продукції не зміниться, а 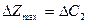 .
.
Інакше розраховується інтервал зміни коефіцієнтів для базисних змінних. У цьому разі зміни відбуваються також у стовпчику 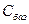 симплекс – таблиці, а це, у свою чергу стосується всіх ненульових оцінок
симплекс – таблиці, а це, у свою чергу стосується всіх ненульових оцінок 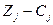 . Так, для базисної змінної
. Так, для базисної змінної 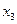 зміна коефіцієнта на величину
зміна коефіцієнта на величину 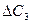 приведе до таких оцінок:
приведе до таких оцінок:
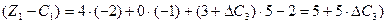
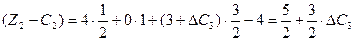
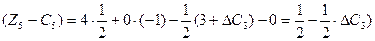
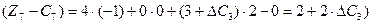
Нові значення оцінок мають задовольняти умову оптимальності, тобто 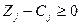 .
.
Тому інтервал для 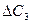 визначається з такої системи нерівностей:
визначається з такої системи нерівностей:
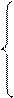
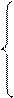
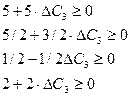
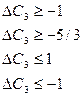
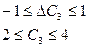
Отже, ціна одиниці продукції С може збільшуватися та зменшуватися на 1 ум. од. і перебувати в межах від 2 до 4 ум. од., але оптимальним планом виробництва продукції залишається: 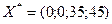 .
.
Для базисної невідомої  інтервал зміни коефіцієнта
інтервал зміни коефіцієнта 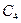 розраховується аналогічно:
розраховується аналогічно:
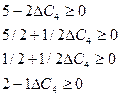
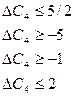
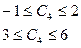
Якщо ціна одиниці продукції Д зменшиться до 3 ум. од. або збільшиться до 6 ум. од., то план виробництва продукції на підприємстві не зміниться 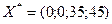 .
.
Якщо ж коливання ціни продукції виходять за визначені межі, то план 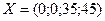 .
.
Вже не буде оптимальним і його необхідно буде покращити згідно з алгоритмом симплекс – методу, тобто продовжити розв’язання задачі.
|
|
Дата добавления: 2014-01-07; Просмотров: 322; Нарушение авторских прав?; Мы поможем в написании вашей работы!