Загальна лінійна модель множинної регресії

Приклади багатофакторний економетричних моделей.

План

Контрольні питання

1.В чому полягає суть регресійного аналізу.

2.В чому полягає суть кореляційного аналізу.

3.Назвіть вимоги до використання кореляційно – регресійного аналізу.

4.Рівняння лінійної однофакторної регресії та її складових.

5.Назвати метод оцінки параметрів лінійної однофакторної регресії.

6.Суть методу найменших квадратів.

7.Дайте означення кореляції.

8.Як можна виміряти силу кореляційного зв’язку?

9.Для чого використовується коефіцієнт детермінації?

10.Поясніть, для чого використовується критерій Фішера?

Тема1.3: «Множинний регресійний аналіз».

1. Приклади багатофакторних економетричних моделей.

2. Загальна лінійна модель множинної регресії.

3. Метод найменших квадратів, основні припущення. МНК-оцінки параметрів лінійної регресії.

Література: [1-16].

На практиці економічний процес змінюється під впливом багатьох різноманітних факторів, які необхідно вміти виявляти та оцінювати.

Розглянемо деякі приклади.

Приклад.1 При розгляді впливу різних соціальних факторів: забезпеченість житлом населення, рівень освіти, продаж алкогольних напоїв на кількість зареєстрованих злочинів в деякій країні протягом n років бачимо, що описати парною регресійною моделлю цей процес не можна. Оскільки на один показник (кількість зареєстрованих злочинів) впливають наступні фактори: забезпеченість житлом населення, рівень освіти, продаж алкогольних напоїв. Доречно було б описувати багатофакторною регресією.

Приклад 2. Розглядаючи реальний валовий продукт, зазначимо, що на нього впливають наступні фактори: кількість робочої сили та кількість витрат на капітал в промисловому секторі країни. Описати і спрогнозувати значення реального валового продукту в наступному періоді можна за допомогою багатофакторної регресійної моделі.

Описати і дослідити зв’язок між економічними показниками можна за допомогою лінійної множинної регресії. Дані залежності є стохастичними і в класичних регресійних моделях встановлюють зв’язок випадкової результативної змінної Y і незалежних змінних: 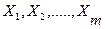у випадку - спостережень.

Стохастична залежність, що визначається лінійною регресією у випадку m пояснюючих змінних може бути виявлена лише при багаторазовому повторенні спостережень. Результати спостереження представляються у вигляді таблиці статистичних даних.

Таблиця №1

Номер спостереження.	Змінні
Залежні	Пояснюючі
і	У	Х1	Х2	…..	Хm
	y1	x11	x12	…..	x1m
	y2	x21	x22	…..	x2m
…..	…..	…..	…..	…..	…..
n	yn	xn1	xn2	….	xnm

Остання залежність має вигляд лінійної регресії у випадку m пояснюючих змінних.

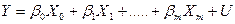(3.1),

Де 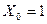- фіктивна змінна; - залежна (пояснювальна) змінна; 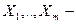незалежні (пояснюючі) змінні; 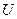- помилки; - невідомі параметри, які потрібно оцінити. Якщо позначити оцінки параметрів через 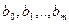, то отримаємо наступне рівняння лінійної багатофакторної регресії:

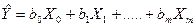(3.2).

Дата добавления: 2014-01-07