Тема: Провідники в електричному полі. Електроємність. Конденсатори

Лекція № 22.

При внесенні будь–якої речовини в електричне поле в речовині відбувається зміщення позитивних і негативних зарядів (ядер і електронів), що у свою чергу приводить до часткового розподілу цих зарядів. У тих або інших місцях речовини з'являються нескомпенсовані заряди різного знака. Це явище називають електростатичною індукцією, а заряди, що з'явилися в результаті перерозподілу – індукованими зарядами.

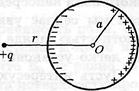Індуковані заряди створюють додаткове електричне поле, що разом з вихідним (зовнішнім) електричним полем утворить результуюче поле. Помістимо металевий провідник у зовнішнє електростатичне поле або надамо йому який–небудь заряд. В обох випадках на всі заряди провідника буде діяти електричне поле, у результаті чого всі негативні заряди (електрони) змістяться проти поля. Таке переміщення зарядів буде продовжуватися до тих пір, поки не установиться визначений розподіл зарядів, при якому електричне поле у всіх точках усередині провідника обернеться в нуль. Таким чином, у статичному випадку електричне поле усередині провідника відсутнє і напруженість поля в ньому дорівнює нулю. Відповідно до теореми Гаусса густина розподілу зарядів усередині провідника також дорівнює нулю. Це означає, що усередині провідника надлишкових зарядів немає. Вони з'являються тільки на поверхні провідника. Відсутність електрополя усередині провідника означає, що потенціал поля в будь–якій точці провідника однаковий і дорівнює потенціалу на його поверхні.

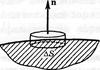Напруженість поля у поверхні провідника. Нехай заряд розподілений по поверхні провідника з поверхневою густиною s. Виділимо циліндр площею S у поверхні провідника. За теоремою Гаусса потік вектора напруженості через виділену поверхню 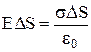. Скоротивши обидві частини отриманої рівності на DS, одержуємо:

.

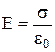Якщо s > 0, то Е > 0, і вектор напруженості спрямований від поверхні провідника, якщо ж s < 0, те Е < 0, вектор напруженості при цьому спрямований до поверхні провідника.

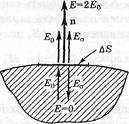Визначимо силу, що діє на поверхню провідника. Розглянемо випадок, коли заряджена ділянка поверхні провідника граничить з вакуумом. На малий елемент dS поверхні провідника діє сила 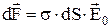, де 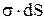– заряд цього елемента, Е₀ – напруженість поля, що створюється всіма іншими зарядами системи в місці перебування заряду 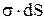. Знайдемо Е₀. Нехай Е_s – напруженість поля, створюваного зарядом на площадці dS у точках, дуже близьких до цієї площадки. Тоді 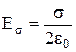. Результуюче поле як усередині, так і поза провідником поблизу площадки dS визначається, як суперпозиція полів Е₀ і Е_s. По різні сторони площадки поле Е₀ практично однакове, а поле Е_s має протилежні напрямки. З умови, що усередині провідника Е = 0 випливає, що Е_s = Е₀, тоді зовні провідника у його поверхні Е = Е₀ + Е_s = 2Е₀. У підсумку одержуємо: 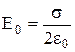і 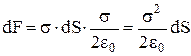. Якщо відома напруженість поля в усіх точках у поверхні провідника 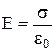, вираження для сили можна переписати у вигляді:

.

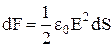Результуюча сила, що діє на весь провідник, визначається інтегруванням останнього рівняння по всій поверхні провідника:

.

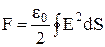Дата добавления: 2014-01-07