Тема: Затухаючи коливання. Автоколивання. Вимушені коливання. Явище резонансу

Лекція № 32.

Практично всяке коливання матеріальної точки, якщо воно не підтримується ззовні, затухає, його амплітуда з часом зменшується. Причинами затухання коливань є сила тертя в точці, де підвішене тіло, сила опору середовища, передавання коливань іншим тілам, теплові ефекти в деформаціях пружин.

Найістотніше впливає на коливання тіла опір середовища. Коли швидкість руху тіла мала, сила опору середовища пропорційна швид­кості: 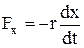, де r – коефіцієнт опору. Знак мінус показує, що сила опору завжди напрямлена проти руху.

Визначимо зміщення як функцію від часу у випадку затуха­ючих коливань. На точку в коливальному русі діють квазіпружна сила і сила опору, тому основне рівняння динаміки має такий вигляд:

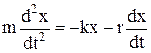. (1)

Масу m, коефіцієнт пружності k і коефіцієнт опору г називають параметрами коливальної системи. Поділивши рівняння (1) на масу m і ввівши заміну і 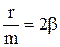, дістанемо однорідне диференціальне рівняння другого порядку:

. (2)

Слід відзначити, що частота w₀ являє собою частоту власних коливань без тертя, її називають власною частотою осцилятора. Коефіцієнт b – коефіцієнт затухання. За умовою b < w₀ рівняння (2) описує затухаючи коливання. Його розв’язок має вигляд: , де А₀ – амплітуда коливань у момент початку спостережень, а – рівняння залежності амплітуди коливань від часу. 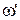– частота затухаючих коливань, яка визначається за формулою: .

З останнього виразу визначаємо умовний період затухаючого коливання:

.

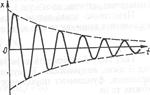Період називається умовним тому, що затухаючі коливання лише умовно можна вважати періодичними – внаслідок зменшення амп­літуди коливання повторюються не абсолютно точно. Період коливання тіла у в'язкому середовищі більший, ніж період його власного коливання. Коли опір середовища значний, коливання не виникає, зміщене тіло повільно без коливання повертається в положення рівноваги. Графік затухаючих коливань зображено на рисунку.

Характеристики затухання:

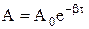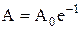- час релаксації – це час, за який амплітуда коливань зменшиться в e разів. Оскільки і , то ;

- логарифмічний декремен­т затухання – логарифм відношення двох послідовних амп­літуд: 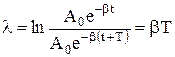. Якщо замість b підставити його значення, то дістанемо: ;

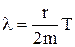- добротність коливальної системи визначається за формулою . Визначає якість коливальної системи.

Щоб коливання не затухали, до системи треба підводити енергію ззовні. Енергію можна поповнювати додатковими зовнішніми пош­товхами в такт коливанням. Практично використовуються такі при­строї, за допомогою яких сама коливальна система в потрібний момент зумовлює зовнішній поштовх. Таку систему називають автоколивальною, а її коливання – автоколиваннями. Прикладом автоколивальної системи є годинник.

Незатухаючі коливання, що виникають під дією зовнішньої періодично змінної сили, називають вимушеними. Нехай зовнішня сила змінюється за гармонічним законом: 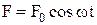. Складемо рівняння динаміки вимушених коливань. При цьому врахуємо, що крім змушувальної сили на систему діють також квазіпружна сила і сила опору середовища, яка пропорційна швидкості руху. Основне рівняння динаміки буде мати такий вигляд:

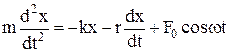(3)

Поділивши це рівняння на масу і ввівши позначення: , , 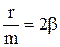, дістанемо неоднорідне лінійне диференціальне рівняння другого по­рядку:

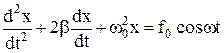(4)

Досвід показує, що через деякий час у системі встановляться гармонічні коливання з частотою змушувальної сили, які відстають по фазі від останньої на j: (5). Задача полягає в знаходженні А і j. Для цього продиференціюємо рівняння (5) два рази:

(6)

(7)

Підставивши рівняння (5), (6) і (7) у (4), одержуємо:

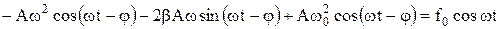(8)

Записавши рівняння (8) для моментів часу, коли і 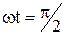, отримуємо систему з двох рівнянь, розв’язуючи які одержуємо:

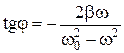(9)

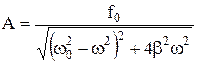(10)

Отже, вирази (5), (9) і.(10) цілком визначають зміщення виму­шених коливань. З отриманих рівнянь свідчить:

- вимушені коливання є гармонічні коливання, частота яких до­рівнює частоті змушувальної сили;

- амплітуда вимушених коливань залежить не тільки від амплі­тудного значення змушувальної сили, а й від її частоти коливання. При певній частоті змушувальної сили w_рез амплітуда вимушених коливань різко зростає, досягаючи максимального значення. Це явище називається резонансом. Резонансну частоту можна визначити з умови максимуму амплітуди або мінімуму підкореневого виразу в знаменнику рівняння (10): 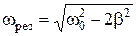. Підставивши це значення час­тоти в (0), знайдемо резонансне значення амплітуди: 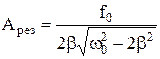. З отриманих виразів свідчить, що коли опір середовища малий 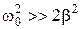, резонансна частота збігається з частотою власних коливань: 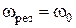. У цьому випадку амплітуда вимушених коливань стає дуже великою. Залежність амплітуди вимушених коливань від частоти і коефі­цієнта затухання зображено на рисунку. Із зростанням коефіцієнта затухання b максимум резонансної кривої швидко опускається і крива згладжується. Явище резонансу стає малопомітним.

Дата добавления: 2014-01-07