Метод гармонической линеаризации

Является приближенным методом исследования режима автоколебаний нелинейных систем. Этим методом можно определить условия возникновения и параметры автоколебаний как в системах второго порядка, так и в более сложных системах

Метод заключается в замене существенного наименьшего элемента с характеристикой f(x_H) эквивалентным линейным звеном с коэффициентом k_H. В замкнутой САУ, работающей в режиме автоколебаний, условием эквивалентности служит равенство амплитуд и фаз выходного сигнала реального нелинейного элемента. При этом предлагается, что сигнал на входе нелинейного элемента является синусоидальным. Такое предположение справедливо во всех случаях, когда линейная часть системы достаточно инерциальная и не пропускает высокочастотные гармоники.

Рассмотрим сущность метода гармонической линеаризации подробнее. Пусть, как и прежде, САУ состоит из отделимых друг от друга линейной и нелинейной частей (рис.16.1), и нелинейная часть описывается уравнением:

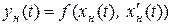(16.1)

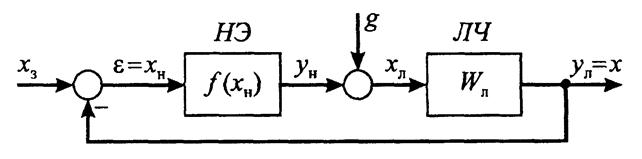
Рисунок 16.1. Типовая структура нелинейной системы

Предположим, что контур системы разомкнут (на выходе линейной части) и что на входе нелинейного элемента действует синусоидальный сигнал

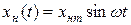(16.2)

При этом на выходе нелинейного элемента будет возникать периодический сигнал 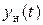, форма которого зависит от характера нелинейности и в общем случае существенно отличается от синусоидальной.

Уравнение нелинейной части (16.1) при синусоидальном воздействии (16.2) можно записать в таком общем виде:

(16.3)

Периодический сигнал 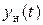может быть разложен в ряд Фурье

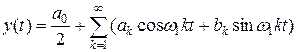
где 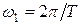- частота основной гармоники;

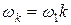- частота k -той гармоники;

коэффициенты 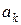и 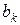определяются по формулам

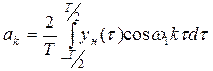, (k = 0, 1, 2,…) (*)

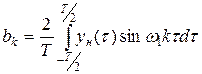, (k = 1, 2,…) (**)

k-тая гармоника выходного сигнала нелинейного элемента имеет вид

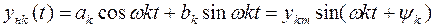(16.4)

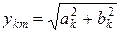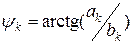; (16.5)

У большинства встречающихся в автоматике нелинейных элементов статическая характеристика кососимметрична относительно начала координат, т. е. и для них всегда постоянная составляющая 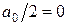, а также коэффициенты всех четных гармоник 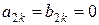и .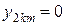

Возможность и правомерность замены реального нелинейного элемента, функционирующего в замкнутой системе в режиме гармонических колебаний, эквивалентным линейным звеном основаны на следующих общих закономерностях:

1. Амплитуды у_кт всех гармоник выше первой почти всегда значительно меньше амплитуды первой гармоники сигнала y_H(t), т.е.

, (k = 3, 5, 7…) (16.6)

2. Линейная часть большинства нелинейных систем обладает свойством фильтра низкой частоты:

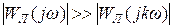, (k = 3, 5, 7…) (16.7)

т. е. все гармоники, кроме основной, существенно ослабляются линейной частью и благодаря этому сигнал y_н(t) на ее выходе окажется близким к синусоиде.

На основании этих двух предпосылок можно при анализе замкнутой системы учитывать только первую гармонику и сигнал y_н(t) на выходе элемента с кососимметричной характеристикой представлять приближенно так:

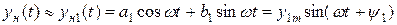(16.8)

Учитывая, что

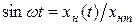; (16.9)

и вводя обозначения

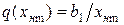
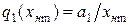(16.10)

можно вместо выражения (8) записать

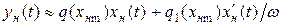(16.11)

или в операторной форме

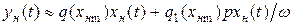(16.12)

Таким образом, при выполнении указанных выше предпосылок нелинейное уравнение (16.3) может быть заменено линейным уравнением (16.11). Эта операция называется гармонической линеаризацией, а коэффициенты 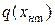и 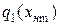- коэффициентами гармонической линеаризации.

Коэффициенты гармонической линеаризации зависят от вида нелинейности и могут быть определены по формулам (*), (**) и (16.9). В таблице 16.1 приведены коэффициенты 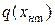и 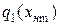для наиболее часто встречающихся нелинейностей.

Гармоническая линеаризация принципиально отличается от обычной линеаризации, т. к. коэффициенты гармонически линеаризованного элемента непостоянны, а зависят от амплитуды входного сигнала 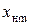. Однако при определенном режиме периодических колебаний, когда значения 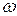и х_нт фиксированы, коэффициенты гармонической линеаризации имеют также постоянные значения. Благодаря этому для решения некоторых задач анализа нелинейных систем могут быть использованы понятия и методы теории линейных систем.

Из уравнения (16.12) можно получить эквивалентную ПФ нелинейного элемента

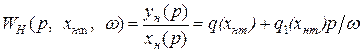(16.13)

а подстановкой в нее 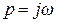- эквивалентную АФХ

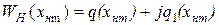(16.14)

Модуль функции (16.14)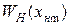

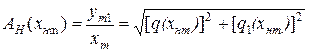(16.15)

определяет отношение амплитуды первой гармоники выходного сигнала к амплитуде входного сигнала, а аргумент функции

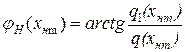(16.16)

- фазовый сдвиг между первой гармоникой и входным сигналом.

Отметим, что у всех нелинейностей с однозначными (статическими) характеристиками коэффициент 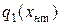равен нулю, и они не создают отставания по фазе.

Таблица 16.1. Коэффициенты гармонической линеаризации типовых нелинейностей

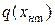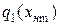На рис.16.2 приведены графики коэффициентов и , построенные по формулам табл. 16.1. Графики построены в безразмерной форме. В качестве единицы измерения амплитуды 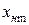принят параметр 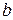, а для самих коэффициентов введен нормирующий множитель 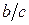или .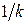

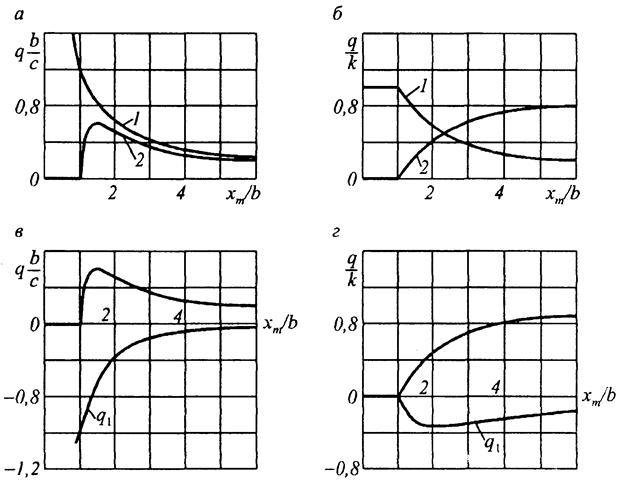
Рисунок 16.2. Зависимости коэффициентов гармонической линеаризации от амплитуды входного сигнала

Линия 1 на рис. 16.2,a соответствует нелинейности 1 в табл. 16.1, линия 2 - нелинейности 2.

Линия 1 на рис. 16.2,б соответствует нелинейности 4, линия 2 - нелинейности 5. На рис. 16.2,в,г представлены графики соответственно для нелинейностей 3 и 6.

У нелинейностей 1-4, имеющих ограничение с, коэффициенты гармонической линеаризации по мере увеличения амплитуды х_нт стремятся к нулю, т. к. амплитуда первой гармоники выходного сигнала остается постоянной. У нелинейностей 5 и 6 с ростом амплитуды х_нт ослабевает влияние нечувствительности 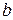, и коэффициент 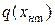стремится к коэффициенту k линейного участка. Нелинейности 3 и 6, имеющие неоднозначные характеристики, создают отставание по фазе. С ростом амплитуды х_нт коэффициент 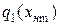этих звеньев уменьшается и соответственно уменьшается отставание по фазе.

Перейдем теперь непосредственно к использованию метода гармонической линеаризации для исследования режима автоколебаний.

Если известны ПФ линейной части

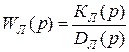(16.17)

и эквивалентная ПФ (16.12) нелинейной части, то можно записать эквивалентную ПФ разомкнутого контура нелинейной САУ

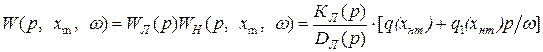(16.18)

и характеристическое уравнение замкнутой гармонически линеаризованной системы

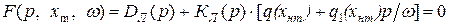(16.19)

В режиме автоколебаний амплитуда х_т и частота 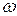остаются постоянными. Следовательно, и функция 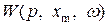в этом режиме постоянна, а выражения (16.18) и (16.19) линейны, и их можно анализировать обычными методами теории линейных САУ.

Существованию в нелинейной САУ автоколебаний соответствует нахождение линеаризованной системы (16.19) на колебательной границе устойчивости. Для определения колебательной границы можно использовать любой из критериев устойчивости, применяемых для линейных систем.

Дата добавления: 2014-01-07