Математическое описание идеального импульсного элемента

Идеальный импульсный элемент представляет собой модулятор. Известно, что выходной сигнал модулятора равен произведению сигнала несущей 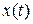на модулирующий сигнал .

Модулирующий сигнал есть последовательность - функций:

.

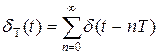С учетом последовательности -функций выражение для выходного сигнала идеального импульсного элемента имеет вид:

.

Определим изображение по Лапласу функции . Для этого произведем некоторые преобразования.

;

.

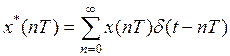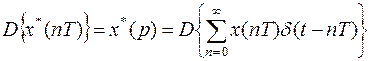Поскольку величина в течение периода Т постоянна, то можно вынести за знак преобразования D

.

Таким образом, изображение по Лапласу сигнала модулированного идеальным импульсным элементом по существу является дискретным изображением по Лапласу решетчатой функции соответствующей непрерывной функции .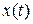

Последнее выражение легко представить в виде z -изображения, применив подстановку :

.

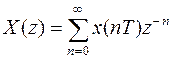Последовательность импульсов можно представить рядом Фурье

,

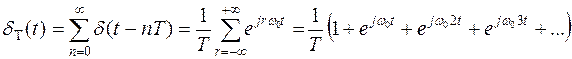где 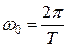- частота импульсов;

r – номер гармоники.

С учетом последнего выражения, сигнал можно записать в виде:

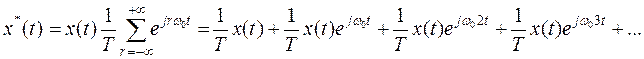
Применив к полученному выражению преобразование Лапласа и, учитывая теорему смещения, получим

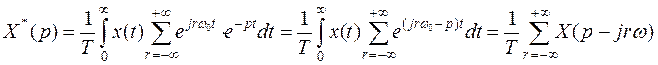
Полученное соотношение устанавливает аналитическую связь между обычным и дискретным преобразованиями Лапласа и получило в литературе название прямого D-преобразования.

Перейдем далее к преобразованию Фурье сигнала .

Преобразование Фурье для k -го члена запишется в виде:

а для всего выражения

.

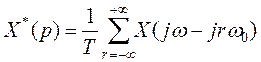Последнее выражение показывает, что частотный спектр решетчатой функции представляет собой сумму частотных спектров модулирующего сигнала, смещенных по оси частот на величины .

Частотный спектр решетчатой функции показан на рис. 22.3.

Рисунок 22.3. Частотный спектр решетчатой функции

Рисунок 22.4. Частотный спектр непрерывного сигнала

Модуляция непрерывным сигналом 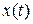последовательности -функций приводит к появлению боковых (дополнительных) полос спектров, идентичных частотному спектру непрерывной функции, около частот, кратных частоте следования импульсов . Реально существуют спектры сигнала, расположенные справа от оси ординат.

Восстановление непрерывной функции, т.е. полезного сигнала может быть произведено по одной из полос спектра. Выделение полезной информации производится фильтрами низких частот, которые отфильтровывают боковые полосы модулированного сигнала. Обычно роль фильтров выполняют сами непрерывные инерционные элементы системы.

Для того чтобы выделить полезную информацию без искажений из модулированного сигнала, необходимо чтобы основной и дополнительные спектры не перекрывали друг друга (рис.22.4, рис.22.5).

Это условие можно сформулировать в виде теоремы, которая носит название теоремы В.А. Котельникова.

Чтобы исходная непрерывная функция была восстановлена без потери информации из модулированного сигнала, необходимо, чтобы частота следования импульсов была не менее чем в 2 раза выше наивысшей частоты 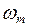в спектре полезного сигнала.

Дата добавления: 2014-01-07