
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Послідовність незалежних випробувань. Формула Бернуллі
|
|
|
|
На практиці доводиться зустрічатись із задачами, які виникають у багаторазово повторюваних випробуваннях, в результаті кожного з яких може з'явитися або не з'явитися подія А. При цьому інтерес уявляє результат не кожного окремого випробування, а загальне число появ події А в результаті певної кількості випробувань. У подібних випадках потрібно вміти визначати ймовірність будь-якого числа m появ події А в результаті n випробувань.
Розглянемо випадок, коли випробування є незалежними й імовірність появи події А в кожному випробуванні однакова й дорівнює р,тоді Р( ) = 1 – р = q. Розглянемо приклад.
) = 1 – р = q. Розглянемо приклад.
Монету підкидають 5 разів. Знайти ймовірність того, що герб з'явиться 3 рази.
Позначимо події:
А - поява герба в одному випробуванні,
В - герб з'явиться 3 рази в серії з п'яти випробувань.
За допомогою алгебраїчних дій подію В можна записати:
В = ААА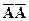 + А
+ А АА
АА + А
+ А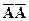 АА +
АА + 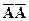 ААА +
ААА +  А
А АА + А
АА + А А
А А +
А +
+ 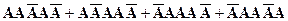
У кожний добуток подія А входить 3 рази, а подія  5-3=2 разів, число додатків дорівнює
5-3=2 разів, число додатків дорівнює 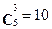 . За формулами додавання й множення одержимо
. За формулами додавання й множення одержимо
Р(В) = Р(ААА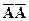 ) + Р(А
) + Р(А АА
АА ) + Р(А
) + Р(А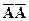 АА) + Р(
АА) + Р(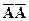 ААА) + Р(
ААА) + Р( А
А АА) +
АА) +
+ Р(А А
А А) + Р(АА
А) + Р(АА А
А ) + Р(А
) + Р(А АА
АА ) + Р(
) + Р( ААА
ААА ) + Р(
) + Р( АА
АА А) =
А) =
= 
 =
= 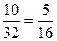 , це і є формула Бернуллі.
, це і є формула Бернуллі.
Запишемо цю формулу в загальному виді. Нехай Р(n,m) – ймовірність того, що в n незалежних випробуваннях подія А наступить m раз. Тоді
Р(n,m) = 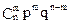 .
.
Доведення формули Бернуллі аналогічне розв’язанню розглянутої вище задачі.
Приклад 9. Вироби деякого виробництва містять 5% браку. Знайти ймовірність того, що серед шести, узятих навмання виробів:
1) буде два бракованих;
2) не буде бракованих;
3) буде хоча б один бракований.
Тут А – поява бракованого виробу, Р(А) = 0,05, Р( ) = 1- 0,05 = 0,95,
) = 1- 0,05 = 0,95,
n=6. За формулою Бернуллі
1) при m = 2, Р(6,2) = 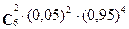 = 0,03;
= 0,03;
2) при m = 0, Р(6,0) = (0,95) 
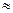 0,73;
0,73;
3) у цьому випадку задачу можна розв’язати двома способами.
Перший спосіб. Використовуючи формулу додавання, одержимо
Р(6,1) + Р(6,2) = 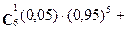
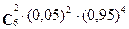
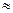 0,27.
0,27.
Другий спосіб. Перейдемо до протилежної події - серед обраних виробів немає бракованих. Ймовірність цієї події обчислена в п.2) і дорівнює 0,73. Тоді шукана ймовірність
Р(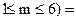 1 – 0,73 = 0,27.
1 – 0,73 = 0,27.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 991; Нарушение авторских прав?; Мы поможем в написании вашей работы!