Лекція 16,17 Довірчий інтервал

Довірчий інтервал () це інтервал, який із заданою ймовірністю p = 1-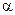містить невідоме значення параметра , тобто

Р(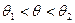) = 1-.

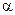Число 1-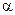називають довірчою ймовірністю, а значення 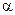- рівнем значущості. Вибір довірчої ймовірності визначається конкретними умовами. Звичайно використовуються значення p = 1-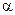, рівні 0,90; 0,95; 0,99.

Один з методів побудови довірчих інтервалів полягає в наступному.

Припустимо,що існує статистика z = z() така, що

1) закон розподілу z відомий і не залежить від ;

2) Функція z() неперервна й строго монотонна по ;

3) нехай p = 1-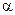- задана ймовірність, а 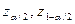- квантилі розподілу статистики z порядків 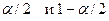. Тоді з імовірністю 1-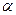виконується нерівність

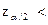z() <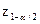. (57)

Ров’язуючи нерівність (57) відносно , знайдемо границі довірчого інтервалу для . Якщо щільність розподілу статистики z, симетричний відносно осі ординат, то довірчий інтервал має найменшу довжину, а якщо розподіл несиметричний, то довжину близьку до найменшої.

Побудуємо довірчий інтервал для математичного сподівання нормально розподіленої генеральної сукупності.

Нехай спостерігається ξ ~ N(a, σ), параметри а й σ - невідомі. Розглянемо статистику

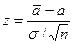
Ця статистика має розподіл Стьюдента з n -1 ступенем волі й, що не залежить від параметра а. Крім того статистика z як функція від а неперервна й строго монотонна. Задамо довірчу ймовірність р =1-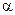. Тоді відповідно до (57) має місце нерівність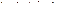

(58)

Ров’язуючи нерівність (58) відносно а й з огляду на властивість (55) квантилей розподілу Стьюдента одержимо, що з імовірністю 1-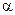виконується умова

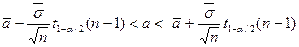, (59)

де 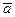й -точкові оцінки, отримані методом підстановки за формулами відповідно (52) і (53), -квантиль розподілу Стьюдента з n-1 ступенем волі.

Знайдемо довірчий інтервал для параметра 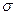. Розглянемо статистику

,

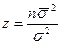вона має розподіл 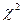з (n-1) ступенем волі, не залежить від параметра 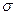, неперервна й монотонна по 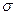. Задамо довірчу ймовірність р =1-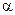, тоді відповідно до (57) має місце нерівність

.

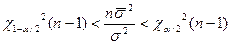Ров’язуючи цю нерівність відносно 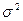, одержимо довірчий інтервал для дисперсії при довірчій імовірності р =1-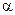

, (60)

де -оцінка параметра дисперсії, отримана за формулою (53), а - за формулою (52).

Якщо розподіл генеральної сукупності не є нормальним, то за вибірками великого обсягу можна побудувати довірчі інтервали для невідомих параметрів приблизно, використовуючи при цьому граничні теореми теорії ймовірностей та асимптотичні розподіли й оцінки, яки з них випливають. Розглянемо приклад.

Нехай в n незалежних випробуваннях подія А наступила m раз. Знайти довірчий інтервал для ймовірності р настання події А. Ефективною оцінкою для р є відносна частота . За теоремою Муавра-Лапласа відносна частота h має асимптотично нормальний розподіл N(p,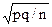), де q = 1 - p.

Розглянемо статистику z =(h-p)/ 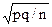, що має асимптотично нормальний розподіл N(0,1) незалежно від значення р. При великих значеннях n має місце наближена рівність

P.

Звідси одержуємо, що з імовірністю 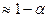виконується нерівність

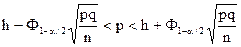. (61)

Заміняючи значення p і q у лівій і правій частинах нерівності (15) їхніми оцінками

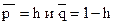, одержуємо, що довірчий інтервал для ймовірності p приблизно має вигляд

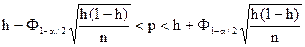. (62)

Приклад 23. При перевірці 100 виробів з великої партії виявлено 10 бракованих деталей. Знайти 95% довірчий інтервал для частки бракованих деталей у всій партії.

Оцінка частки бракованих деталей у партії за вибіркою дорівнює 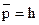=10/100=0,1.

За таблицею Додатка 1 знайдемо квантиль 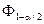= 1,96. За формулою (16) 95%-довірчий інтервал для частки бракованих деталей у партії приблизно має вигляд

0,1- 1,96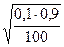< p < 0,1 + 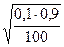і остаточно 0,041 < p < 0,159.

Наближений довірчий інтервал для параметра 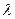в розподілі Пуассона має вигляд

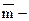
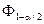
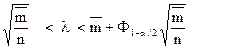(63)

Приклад 24. На кожній з 36 АТС міста в період із двох до трьох годин було зафіксовано в середньому 2 виклика. Вважаючи, що число викликів для кожної АТС має розподіл Пуассона з тим самим параметром 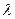, приблизно знайти довірчий інтервал для 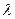з довірчою ймовірністю 0,9.

За умовами задачі 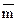= 2, 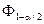==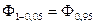 1,645. За формулою (63) одержимо

2 - 1,645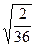< < 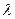2 + 1,645 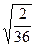або

1,61 < < 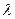2,39

Дата добавления: 2014-01-07