Диференціальних рівнянь частинних похідних

МЕТОД ПРЯМИХ РОЗВ‘ЯЗУВАННЯ ГРАНИЧНИХ ЗАДАЧ ДЛЯ

Суть методу прямих:

Нехай в прямокутній області: 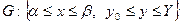задане наступне рівняння:

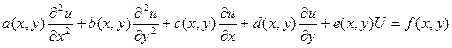
де: 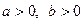в області 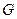і на їх межі.

Нехай розв‘язок рівняння (1) задовольняє також граничні умови:

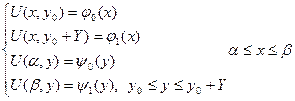(2)

де: 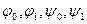- задані.

По осі 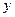виберемо точки і проведемо прямі .

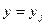В рівнянні (1) замість змінної 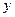будемо записувати 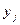і замінимо похідні по 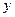наступними різницевими співвідношеннями:

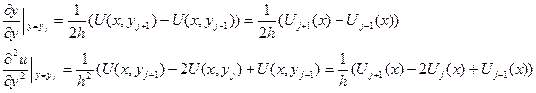
Підставивши в (1) маємо:

(3)

а також крайові умови:

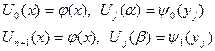(4)

Систему (3) і (4) називають системою рівнянь методу прямих.

Загальний розв‘язок системи диференціального рівняння (3) буде залежати від 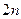довільних сталих.

Використовуючи граничні умови (4) для відшукання цих сталих отримаємо систему 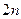лінійних алгебраїчних рівнянь, розв‘язавши їх знайдемо наближення розв‘язку рівняння на прямих .

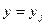Зауваження: 1) Метод прямих зручно використовувати тоді коли коефіцієнти в рівнянні (1) незалежні від х.

3) Метод прямих зручно використовувати як граничний випадок методу сіток, якщо в прямокутній сітці крок по х спрямувати до 0.

Дата добавления: 2014-01-07