Індивідуальні завдання до заняття 8

Розділ 9.1. Математичне сподівання неперервної випадкової величини

Нехай неперервна випадкова величина Х задана диференціальною

функцією f(х).

Припустимо, що всі значення Х належать відрізку [a,b]. Розіб’ємо цей відрізок на m частин Δх₁, Δх_2,.. Δх_n, які не перетинаються і . Виберемо на кожному з елементарних відрізків по одній точці ). Користуючись формулою математичного сподівання для дискретної випадкової величини, запишемо наближене значення математичного сподівання величини

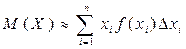. (9.1)

Суму (9.1) можна розглядати, як інтегральну суму, тому, переходячи до границі при отримаємо формулу математичного сподівання неперервної випадкової величини

.

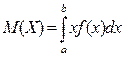Означення: Математичним сподіванням неперервної випадкової величини Х, можливі значення якої належать відрізку , називають визначений інтеграл

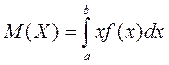. (9.2)

Якщо неперервна випадкова величина задана на всій числовій осі, тобто 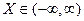, тоді

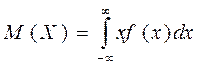. (9.3)

Дата добавления: 2014-01-07