Задачі до розділу 9.1

Задача 9.1.1

Випадкова величина Х задана диференціальною функцією (щільністю розподілу) f(x)=2x в інтервалі (0, 1), зовні цього інтервалу f(x)=0. Знайти математичне сподівання випадкової величини Х.

Рішення

Використаємо формулу (9.3)

.

.

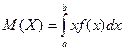Задача 9.1.2

Випадкова величина Х задана диференціальною функцією (щільністю розподілу) f(x)=0,5x в інтервалі (0, 2), зовні цього інтервалу f(x)=0. Знайти математичне сподівання випадкової величини Х.

Задача 9.1.3

Знайти математичне сподівання неперервної випадкової величини Х, що задана інтегральною функцією

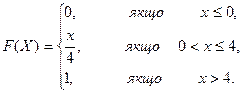
Розділ 9.2. Дисперсія та середнє квадратичне відхилення неперервної випадкової величини

За аналогією до дисперсії дискретної неперервної величини визначається і дисперсія неперервної випадкової величини.

Означення: Дисперсією неперервної випадкової величини Х, заданої на відрізку [а,b], називається математичне сподівання квадрата її відхилення від математичного сподівання

. (9.4)

Аналогічно для випадку, коли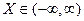

. (9.5)

Після перетворення інтегралу (9.4) отримаємо

.

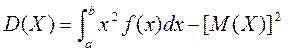Якщо ж позначити

,

то формула (9.4) запишеться у вигляді

D(X)=M(X²)-[M(X)]². (9.6)

Аналогічним буде вираз для дисперсії, якщо 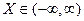, тільки треба брати

а М(Х) за формулою (9.2) із розділу 9.1.

Означення: Середнє квадратичне відхилення неперервної випадкової величини дорівнює кореню квадратному із дисперсії неперервної випадкової величини:

. (9.7)

Приклад:

Знайти математичне сподівання і дисперсію неперервної випадкової величини, заданої інтегральною функцією F(x), якщо

Рішення

Знайдемо відповідну диференціальну функцію

тоді

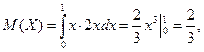
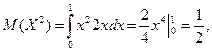
Дата добавления: 2014-01-07