Гидравлика 3 страница

2.5. Неньютоновские жидкости

Простейшей моделью жидкостей или газов является идеальная жидкость, при движении которой отсутствуют касательные напряжения. Тензор напряжения в этом случае является сферическим, т.е

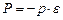, (2.26)

где 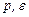- давление и тензорная единица, соответственно.

Выражение (2.26) представляет собой простейший вид реологического уравнения среды. Реологическое уравнение среды связывает компоненты тензоров напряжений, деформаций и их производных по времени; при этом тензор скоростей деформаций представляет собой производную по времени от тензора деформаций. Уравнение (2.26) показывает, что все нормальные напряжения в данной точке среды выражаются через одну скалярную величину - давление.

Реологический закон текучести для реальной (вязкой) жидкости, находящейся в прямолинейном ламинарном движении, основан на гипотезе Ньютона, утверждающей существование прямой пропорциональности между касательными напряжениями 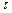, действующими в плоскостях соприкасания слоев жидкости, и производными от скорости u по направлениям, нормальным к этим плоскостям (по n). Он имеет вид

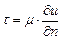. (2.27)

Здесь 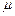- коэффициент пропорциональности (зависит от температуры жидкости) или динамический коэффициент вязкости.

Из формулы (2.27) следует, что 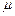- касательное усилие, приходящееся на единицу площади и приложенное к слоям жидкости, отстоящим друг от друга на расстоянии, равном единице длины при единичной разности скоростей между ними.

Реологический закон (2.27) представляет собой частный случай более общего закона линейной связи между тензором напряжений и тензором скоростей деформаций. Этот закон называется обобщенным законом Ньютона. Для несжимаемой вязкой жидкости обобщенный закон Ньютона имеет вид

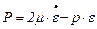, (2.28)

где 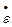- тензор скоростей деформаций.

Компоненты тензора напряжений составляют

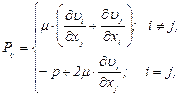(2.29)

где 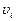- составляющие вектора скорости.

Жидкости, удовлетворяющие обощенному закону вязкого трения Ньютона называются ньютоновскими жидкостями.

Для ньютоновских жидкостей вязкость не зависит от скорости сдвига. Зависимость между напряжением и скоростью деформации представляет собой прямую линию (рис. 2.6, прямая 3) с тангенсом угла наклона .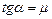

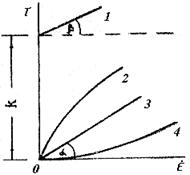
1 - вязко-пластическая; 2- псевдопластическая;

3 - ньютоновские жидкости; 4 - дилатантные среды

Рис. 2.6. Связь между напряжением сдвига 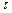и скоростью

деформации 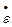для разных текучих сред

В ньютоновских жидкостях диссипация энергии обусловлена столкновением небольших молекул. Поэтому к числу ньютоновских жидкостей относятся все жидкости, газы, растворы с небольшой молекулярной массой.

Жидкости, не подчиняющиеся в своем движении обобщенному закону Ньютона, называются неньютоновскими. К ним относятся, например, смазки, которые не текут при малом давлении до тех пор, пока не будет достигнут достаточно большой перепад давления. Максимальное напряжение, которое необходимо иметь для того, чтобы происходило течение таких жидкостей, как смазки, называется пределом текучести ().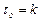

При напряжении сдвига, превосходящем предел текучести (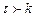) скорость сдвига становится пропорциональной разности между приложенным напряжением и пределом текучести (рис. 2.6, прямая 1).

, (2.30)

Здесь 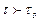, 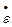- скорость сдвига; .

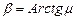Зависимость (2.30) была предложена в 1889 г. Ф.Н. Шведовым, в 1916 г. ее получил Е. Бингам. Среды, течение которых характеризуется реологическим уравнением (2.30), называются средами Шведова-Бингама (вязко-пластические среды или тела).

Предполагается, что вязко-пластические среды имеют пространственную структуру, достаточно жесткую, чтобы сопротивляться напряжению, не превосходящему предела текучести. Если 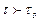, происходит разрушение этой структуры. При среда начинает течь как обычная ньютоновская жидкость (рис. 2.6, прямая 3). При 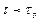структура материала среды восстанавливается.

Связь между тензорами - девиаторами напряжений 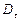и скоростей деформаций 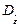, согласно (2.30), выражается следующим образом

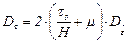, (2.31)

где H - интенсивность скоростей деформаций сдвига,

.

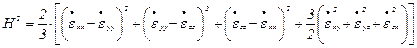К числу неньютоновских жидкостей относятся, кроме вязко-пластических сред, жидкости, не обнаруживающие предела текучести, но с увеличением скорости течения приобретающие измененную текучесть. При продавливании таких жидкостей через капилляр увеличение давления вдвое может вызвать четырехкратное повышение их расхода. Такие жидкости называются псевдопластичными или разжижающимися под действием сдвига (рис. 2.6, кривая 2).

При высоких скоростях сдвига псевдопластичные жидкости напоминают вязко-пластичные тела Шведова-Бингама, а при низких скоростях они ведут себя подобно ньютоновским жидкостям. Такое поведение материала можно объяснить тем, что при низких скоростях сдвига несферические полимерные частицы распределяются хаотически, а при повышении скорости они стремятся ориентироваться в направлении течения. И это является причиной уменьшения сопротивления их обтеканию.

Обратное явление, сводящееся к загущению системы при течении, свойственно так называемым дилатантным материалам. Для этих материалов повышение перепада давления в четыре раза приводит к увеличению скорости их течения лишь вдвое. Возможны и иные соотношения между перепадом давления и скоростью течения при сохранении дилатантного течения (рис. 2.6, кривая 4).

При течении дилатантной среды в случае малых скоростей сдвига ее частицы скользят друг по другу. С постепенным повышением скорости сдвига одни частицы начинают препятствовать движению других, перемещающихся более быстро, в результате чего быстродействующие частицы перескакивают через соседние частицы. Такой процесс эквивалентен расширению системы. Таким образом, процесс структурообразования является причиной нарастания вязкости при увеличении скорости сдвига.

Для описания дилатантных и псевдопластичных жидкостей установлена эмпирическая функциональная зависимость в виде степенного закона Оствальда

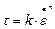, (2.32)

где k - мера консистенции жидкости (чем выше вязкость жидкости, тем больше k);

n - индекс течения, который определяет степень отличия течения неньютоновской от ньютоновской среды.

В общем случае n не является постоянной величиной. Размерность величины k зависит от n. Обычно в расчетах n и k принимают постоянными. Очевидно, что при n = 1 имеет место среда, подчиненная в своем движении обобщенному закону Ньютона, при этом коэффициент k характеризует динамическую вязкость среды.

Пользуясь формулами (2.28) и (2.32), можно получить выражение для так называемой кажущейся вязкости

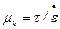, (2.33)

где .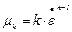

Это позволяет записать степенной закон Оствальда в виде, напоминающем гипотезу Ньютона

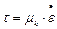. (2.34)

Связь между компонентами тензора напряжений и тензора скоростей деформаций для несжимаемых жидкостей, подчиненных степенному закону течения, выражается в следующей форме

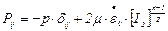, (2.35)

где 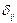- символ Кронекера,

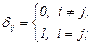
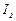- второй инвариант тензора скоростей деформации.

Квадратичный (второй) инвариант тезора-девиатора скорости деформации 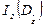представляет собой суммарную характеристику искажения формы элемента среды.

Движение неньютоновских вязких несжимаемых жидкостей, как и ньютоновских, в каналах различных сечений возможно лишь при наличии перепада давления между сечениями канала. Наличие перепада давления выражается суммой двух совершенно различных, по своей физической природе слагаемых. Одно на них представляет собой изменение давления, обусловленное изменением кинетической энергии движущейся массы жидкости, другое, (необратимая часть) - изменение давления вследствие диссипации энергии (преобразования механической энергии в тепловую).

При движении несжимаемой жидкости по каналу постоянного сечения изменение давления, обусловленное изменением кинетической энергии жидкости, может возникнуть на участке стабилизации потока. В области стабилизировавшегося течения (поле скоростей от сечения к сечению неизменно) остается лишь необратимая часть перепада давления (она поддерживает существование установившегося течения). В области установившегося течения необратимая часть перепада давления (перепад давления) является мерой гидравлического сопротивления. Количественной характеристикой гидравлического сопротивления служит коэффициент гидродинамического (гидравлического) сопротивления.

К неньютоновским жидкостям относятся и дисперсные среды - смеси двух фаз, одна из которых (основная) является сплошной, а вторая, дисперсная, распределена в первой в виде отдельных элементов объема. Как правило, основная фаза может быть или жидкостью, или газом, дисперсная фаза - жидкостью, твердым телом или газом.

Если основная фаза представляет собой жидкость, то она может содержать взвешенные твердые частицы (суспензия), капли другой, не смешивающейся жидкости (эмульсия), газовые пузырьки или полости (кипящая жидкость или пена).

К неньютоновским жидкостям также относят многие биологические жидкости, например, кровь, представляющую собой суспензию деформирующихся кровяных телец - эритроцитов диаметром около 8 мкм, окруженных прозрачной ньютоновской жидкостью - плазмой. Вязкость крови существенно уменьшается при увеличении ее скорости деформации. Каждая суспензия обнаруживает этот эффект.

Для установившегося движения перечисленных сред необходимо поддержание неравного нулю перепада давления. И главную роль в этом играет наличие вязкости, как основной характеристики реальных жидких сред.

2.6. Термические уравнения состояния

Термическим уравнением состояния среды устанавливается связь между давлением, плотностью и температурой Т в данной точке потока

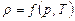. (2.36)

Если рабочей средой является газ, который можно считать совершенным, то зависимость (2.36) приводит к уравнению Клапейрона

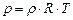, (2.37)

где Т - температура, Кельвин;

R - газовая постоянная, имеющая различные значения для разных газов; для воздуха .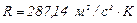

Газы, применяемые в пневмосистемах, считаются совершенными, что согласуется с экспериментальными данными в тех диапазонах давлений и температур, при которых работает большинство пневмосистем. При использовании воздуха или азота давления предполагаются ограниченными значениями, не превышающими 20 МПа при температурах больше критической.

Вследствие изменения объема, занимаемого газом, изменения давления или температуры газ переходит из одного состояния в другое. Такой процесс называется термодинамическим. Для описания термодинамического процесса уравнение состояния газа должно быть дополнено уравнением сохранения энергии. В общем случае для решения этих уравнений необходимо еще использовать законы притока тепла, что, как уже отмечалось, может значительно усложнить задачу. Поэтому часто принимаются дополнительные допущения, при которых заранее устанавливаются виды некоторых идеализированных термодинамических процессов. К ним относятся изотермические и адиабатные процессы.

Процесс, при котором благодаря интенсивному теплообмену температура газа остается постоянной, называется изотермическим. Действительный процесс будет тем ближе к изотермическому, чем медленнее изменяется состояние газа и лучше условия теплообмена с окружающей средой (Т = const).

Процесс, происходящий без теплообмена между газом и окружающей его средой, называется адиабатным. К адиабатным приближаются такие действительные процессы, при которых вследствие хорошей теплоизоляции объема, занятого газом, или вследствие быстроты протекания процесса теплообмен не оказывает сколько-нибудь существенного влияния на состояние газа. Уравнение адиабатного процесса имеет вид

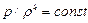. (2.38)

Величина k в уравнении (2.38) называется показателем адиабаты; если адиабатный процесс рассматривать без учета внутреннего трения (изоэнтропический адиабатный процесс), то

, (2.39)

где и - удельные теплоемкости газа соответственно при постоянном давлении и при постоянном объеме.

Характеристикой термодинамического процесса может служить некоторая величина, показывающая, какую часть теплоты, участвующей в процессе, составляет изменение внутренней энергии. Любой процесс, в котором эта величина имеет определенное значение, называется политропным. Для политропного процесса

, (2.40)

где n - показатель политропы.

Уравнения рассмотренных выше процессов можно получить из уравнения (2.40), принимая для изотермического процесса n = 1, а для адиабатного n = k.

Известно, что скорость 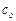звука в сжимаемой среде определяется зависимостью

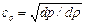. (2.41)

Предположив, что изменение плотности газа, сопровождающее распространение звуковой волны, происходит изоэнтропически, получаем

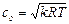. (2.42)

Из соотношения (2.42) следует, что скорость распространения звука в идеальном газе зависит только от абсолютной температуры.

Экспериментальными исследованиями для большинства жидкостей установлена зависимость модулей объемной упругости от давления и температуры. Поэтому для жидкостей связь между изменением плотности и давлением определяется обычно с помощью модуля объемной упругости, причем влияние температуры учитывается в самом модуле упругости. При малом процентном содержании нерастворенного газа в жидкости применяются такие же зависимости, как для жидкости, не содержащей газа, но значение модуля объемной упругости корректируется. Эти зависимости могут быть использованы вместо уравнения состояния и для газа, когда принимается допущение об изотермическом или адиабатном характере термодинамического процесса. В рассмотренных случаях необходимое термическое уравнение состояния для жидкостей записывается в виде

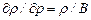, (2.43)

где В - модуль объемной упругости среды.

Модуль объемной упругости жидкости можно измерить двумя методами. Первый метод основывается на применении устройств, позволяющих определять относительные изменения объема жидкости в зависимости от изменения давления при заданной температуре. Полученный при таких экспериментах модуль объемной упругости жидкости называется изотермическим. При втором методе в жидкости возбуждаются колебания давления с соблюдением условий, позволяющих пренебречь процессами теплообмена; полученный этим методом модуль объемной упругости жидкости называется адиабатическим.

2.7. Растворимости газов в жидкостях, кипение,

кавитация. Смеси.

Растворимость газов в жидкостях характеризуется количеством растворенного газа в единице объема жидкости, различна для разных жидкостей и изменяется с увеличением давления.

Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно подсчитать по закону Генри, т.е.

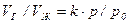, (2.44)

где 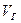- объем растворенного газа, приведенный к нормальным условиям ();

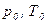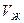- объем жидкости;

k - коэффициент растворимости;

р - давление жидкости.

При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворяется в ней. Это явление может отрицательно сказываться на работе гидросистем.

В результате испарения жидкость переходит в пар. Испаряемость свойственна всем капельным жидкостям и зависит от температуры и давления. Одним из показателей, характеризующих испаряемость жидкости, является температура ее кипения при нормальном атмосферном давлении; чем выше температура кипения (процесса парообразования в толще жидкости), тем меньше испаряемость жидкости. Однако интенсивность испарения неодинакова у различных жидкостей и зависит от условий, в которых они находятся. В гидросистемах нормальное атмосферное давление является лишь частным случаем; обычно приходится иметь дело с испарением, а иногда и кипением жидкостей в замкнутых объемах при различных температурах и давлениях.

Кипение капельной жидкости при заданной температуре может быть получено понижением давления. Давление, при котором происходит кипение жидкости, называют давлением парообразования. Наименьшее давление, при котором происходит кипение при нормальной температуре, называют давлением насыщенных паров. Чем больше давление насыщенных паров, тем больше испаряемость жидкости (рис. 2.7).

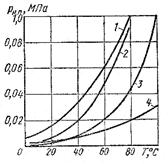
1 - бензин Б-70; 2 - спирт; 3 - вода; 4 - керосин

Рис. 2.7. Зависимость давления насыщенных паров

жидкостей от температуры

Кавитацией называется нарушение сплошности потока жидкости, обусловленное появлением в ней пузырьков или полостей, заполненных паром или газом. Кавитация возникает при понижении давления, в результате чего жидкость закипает или из нее выделяется растворенный газ. В потоке жидкости такое падение давления происходит обычно в области повышенных скоростей. В большинстве случаев жидкость настолько быстро проходит через область пониженного давления, что газ не успевает выделиться. В этом случае кавитацию часто называют паровой. Полости или пузырьки, заполненные паром, увлекаются потоком в область повышенного давления. Здесь пар конденсируется и полости, заполненные паром, замыкаются.

В качестве меры, определяющей кавитационные свойства профилей, применяют так называемое число кавитации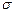

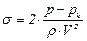, (2.45)

где р и V - соответственно давление и скорость в набегающем потоке.

Появление кавитации всегда вызывает увеличение сопротивления, т.е. добавочную потерю энергии. Кроме этого, она влечет за собой кавитационную коррозию металла и появление кавитационных шумов. Все эти вредные действия кавитации настолько существенны, что обычно при проектировании насосов, турбин и винтов лопасти рассчитывают так, чтобы на них не возникала кавитация.

Смеси из нескольких тел (газообразных или жидких) могут быть получены одним из следующих трех основных способов смешивания: смешивание в объеме; смешивание в потоке и смешивание в случае заполнения объема потоком. Обычно приводят рассуждения о смешивании лишь двух веществ или компонентов, а другие более сложные случаи сводят затем к последовательному добавлению нового компонента к уже имеющейся смеси. Для бинарной смеси, состоящей из компонентов а и b, в единице объема смеси содержится масса 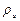компонента а и масса 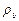компонента b. Величины 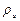и 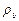называют плотностями компонентов, которые удовлетворяют соотношению

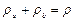, (2.46)

где 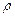- плотность смеси.

Безразмерные величины 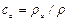и 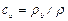представляют собой массовые концентрации компонентов а и b в смеси и удовлетворяют соотношению

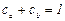. (2.47)

Парциальные энтальпии компонентов газовых и жидких смесей (количество теплоты в единице массы компонента а или b), близких к идеальным (отсутствует заметная теплота смешивания), равны значениям энтальпий чистых веществ а и b. Энтальпия смеси h (количество теплоты в единице массы смеси) связана с величинам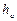и и 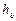соотношением

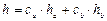. (2.48)

При смешивании компонент через контрольную поверхность пространства осуществляется перенос массы веществ а и b с разной интенсивностью. Количественной характеристикой таких процессов служит вектор плотности потока массы смеси (импульс единицы объема смеси), который складывается из векторов плотности потоков массы компонентов а и b. Вектор конвективной скорости движения смеси как сплошной среды (импульс единицы массы смеси) определяется отношением вектора плотности потока массы смеси к плотности смеси.

В случае фазовых смесей границы раздела фаз (в рамках представлений сплошной среды) интерпретируются как геометрические поверхности. Реальные межфазные границы - это тонкие переходные слои сложной структуры. Молекулы, составляющие переходный слой, взаимодействуют с молекулами обеих граничащих фаз, в силу чего свойства переходного слоя отличаются от свойств вещества в объемах фаз. Поэтому при интерпретации границы раздела фаз как геометрической поверхности ей приписываются некоторые феноменологические свойства.

Коэффициент теплопроводности смеси зависит от концентрации компонентов, а динамическая вязкость смеси - от вязкости чистых компонентов, концентрации и физической природы смеси. При смешивании идеальных газов параметры смеси определяют в соответствии с аддитивностью термодинамических величин газов, составляющих смесь.

2.8. Законы переноса

При изучении потоков жидкостей и газов обычно рассматривается перенос трех величин: одной векторной (количества движения) и двух скалярных (тепла и вещества). В движущемся потоке, в общем случае, наблюдается неоднородность таких величин, как скорость, температура и концентрация вещества. Вследствие наличия этих неоднородностей в среде возникают явления переноса количества движения, тепла и массы.

Если в потоке выделить некоторый элементарный объем, то по его поверхности будут действовать касательные и нормальные силы. Касательные силы возникают вследствие наличия внутреннего трения или вязкости. Как известно из физики, Ньютон сформулировал закон переноса количества движения молекул, согласно которому касательное напряжение трения между двумя слоями прямолинейно движущейся вязкой жидкости пропорционально отнесенному к единице длины изменению скорости по нормали к направлению движения

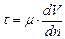. (2.49)

Коэффициент пропорциональности 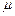в уравнении (2.49) называется динамическим коэффициентом вязкости. Как известно, динамический коэффициент вязкости не зависит от давления и от характера движения, а определяется лишь физическими свойствами жидкости и ее температурой.

Законы переноса тепла и массы имеют вид, аналогичный закону Ньютона. Например, закон Фурье для переноса тепла будет

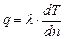, (2.50)

а закон Фика для переноса вещества

, (2.51)

где q и - количество тепла и вещества, переносимого через единицу площади в единицу времени;

Т и с - температура и концентрация вещества.

Коэффициенты пропорциональности и D называются соответственно коэффициентами теплопроводности и диффузии. Коэффициенты и D зависят только от физических свойств среды и температуры.

По своей структуре все существующие потоки реальной вязкой жидкости делятся на ламинарные и турбулентные. При ламинарном или слоистом движении подкрашенные струйки остаются резко выделенными во все время движения, т.е. отдельные частицы движутся по определенным траекториям. При турбулентном движении отдельные частицы жидкости совершают беспорядочное движение по хаотически переплетенным и быстро изменяющимся траекториям. От структуры потока существенно зависят все процессы переноса, т.е. величины, характеризующие процесс переноса количества движения, тепла и вещества. В силу этого законы переноса, приведенные выше, пригодны лишь для ламинарных потоков, при турбулентном движении процессы переноса значительно сложнее.

2.9. Требования к рабочим жидкостям

Физические и эксплуатационные свойства рабочих жидкостей должны удовлетворять целому комплексу требований, среди которых можно назвать следующие:

- широкий диапазон возможных температур. Верхняя граница этого диапазона ограничена температурой самовозгорания жидкости и возможностью ее расслоения или химического распада. Нижняя граница определяется предельно допустимыми значениями вязкости жидкости;

- возможность длительной эксплуатации с большими давлениями, обусловленными жесткими условиями по минимальным габаритам и весу гидроагрегатов;

- достаточно высокая объемная прочность жидкости, которая характеризуется давлением насыщенного пара этой жидкости при различных температурах. При уменьшении фактического давления в жидкости ниже давления парообразования происходит испарение жидкости в образующиеся пузыри, т.е. разрыв сплошности жидкости;

- хорошая смазывающая способность для уменьшения износа деталей и снижения сил трения между ними, влияющих на характеристики агрегатов;

- химическая нейтральность к материалам деталей агрегатов: металлам, их покрытиям, резине и пластмассам. Отсутствие кислот, разрушающих железные детали, и щелочей, реагирующих с цветными металлами;

Дата добавления: 2014-01-06